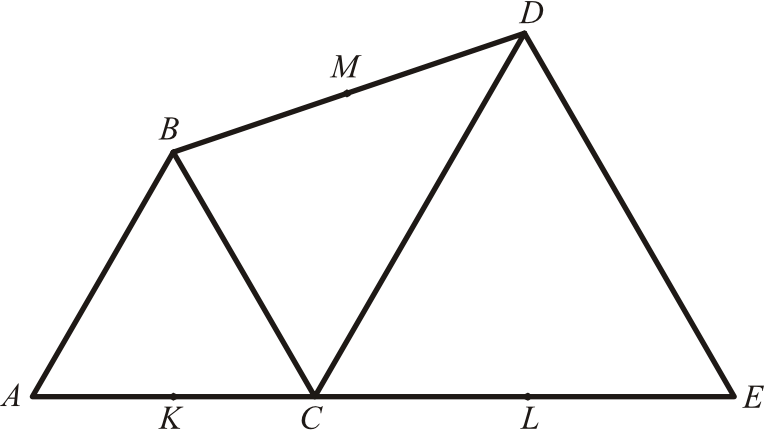
Trójkąty \(ABC\) i \(CDE\) są równoboczne. Punkty \(A\), \(C\) i \(E\) leżą na jednej prostej. Punkty \(K\), \(L\) i \(M\) są środkami odcinków \(AC\), \(CE\) i \(BD\) (zobacz rysunek). Wykaż, że punkty \(K\), \(L\) i \(M\) są wierzchołkami trójkąta równobocznego.

Odpowiedź:      

Udowodniono wykorzystując własności trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Połączmy sobie punkty \(K\), \(L\) oraz \(M\) - tworzą one wierzchołki trójkąta, którego cechę równoboczności musimy udowodnić. Skoro trójkąty \(ABC\) i \(CDE\) są równoboczne, to możemy na rysunek nanieść też ich miary \(60°\). Krok 2. Dostrzeżenie par odcinków równoległych. Zarówno bok \(AB\) jak i \(CD\) są nachylone do podstawy czworokąta \(AEDB\) pod kątem \(60°\). To oznacza, że te odcinki są względem siebie równoległe, czyli \(AB||CD\). Punkty \(K\) oraz \(M\) dzielą odcinki łączące te dwie proste równoległe dokładnie w połowie swojej długości, stąd też odcinek \(KM\) jest równoległy do odcinków \(AB\) i \(CD\), a więc i on jest nachylony do podstawy czworokąta pod kątem \(60°\). Ta zależność wynika także z Twierdzenia Talesa. Wiemy już więc, że \(\sphericalangle MKL=60°\). Analogicznie sytuacja wygląda po drugiej stronie czworokąta. Odcinki \(CB\) oraz \(ED\) są nachylone do podstawy czworokąta pod tym samym kątem \(60°\), są więc względem siebie równoległe. Odcinek \(ML\) jest równoległy względem zarówno odcinka \(CB\) jak i \(ED\) (dokładnie z tego samego powodu o jakim mówiliśmy powyżej, analizując odcinek \(KM\)), a więc \(\sphericalangle MLK=60°\). Dwa kąty w trójkącie KLM mają miarę \(60°\) więc i trzeci kąt musi mieć \(60°\), czyli jest to trójkąt równoboczny.

Teoria:      
W trakcie opracowania