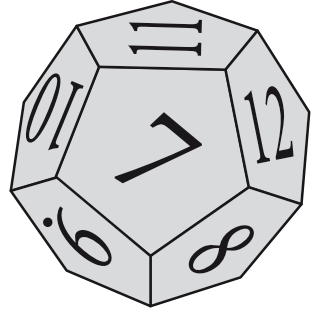
Na ściankach symetrycznej dwunastościennej kostki do gry zapisano liczby \(1, 2, 3,..., 12\) (jak na rysunku). Rzucamy tą kostką trzy razy i zapisujemy wyrzucone liczby w kolejności otrzymywania, tworząc ciąg trójwyrazowy. Oblicz prawdopodobieństwo zdarzenia, że utworzymy w ten sposób ciąg geometryczny o ilorazie całkowitym. Uwaga. Ciąg stały jest ciągiem geometrycznym.

Odpowiedź:      

\(P(A)=\frac{1}{108}\)

Rozwiązanie:      
Krok 1. Obliczenie liczby wszystkich zdarzeń elementarnych. Rzucamy trzykrotnie dwunastościenną kostką. W każdym rzucie możemy otrzymać jeden z dwunastu wyników, zatem wszystkich zdarzeń elementarnych zgodnie z regułą mnożenia będziemy mieć: $$|Ω|=12\cdot12\cdot12=1728$$ Krok 2. Obliczenie liczby zdarzeń sprzyjających. Zdarzeniem sprzyjającym jest sytuacja w której wylosowane liczby utworzą ciąg geometryczny, czyli przykładowo takimi zdarzeniami mogą być \(2,4,8\) lub też \(1,3,9\). Musimy wypisać wszystkie możliwe warianty. Warto tutaj zwrócić uwagę, że iloraz \(q\) w takich ciągach musi być liczbą naturalną. Jakbyśmy mieli \(q\) w postaci liczby niecałkowitej (np. w postaci ułamka typu \(\frac{1}{2}\)) to w ciągu będą pojawiać nam się liczby niecałkowite, a takich na kości nie mamy. Najprościej będzie wypisać wszystkie warianty w następujący sposób: Gdy \(q=1\): \((1,1,1), (2,2,2), (3,3,3),..., (12,12,12)\) Mamy więc tutaj \(12\) takich zdarzeń. Gdy \(q=2\): \((1,2,4), (2,4,8), (3,6,12)\) Mamy więc tutaj \(3\) takie zdarzenia. Gdy \(q=3\): \((1,3,9)\) Mamy więc tutaj \(1\) takie zdarzenie. Łącznie zdarzeń sprzyjających mamy zatem: $$|A|=12+3+1=16$$ Krok 3. Obliczenie prawdopodobieństwa. $$P(A)=\frac{|A|}{|Ω|}=\frac{16}{1728}=\frac{1}{108}$$

Teoria:      
W trakcie opracowania