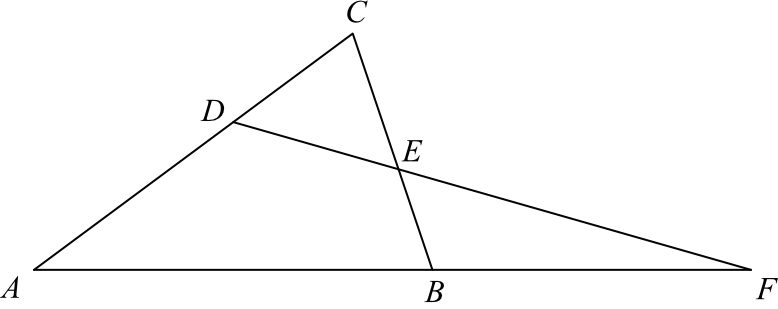
Dany jest trójkąt \(ABC\), w którym \(|AC|\gt|BC|\). Na bokach \(AC\) i \(BC\) tego trójkąta obrano odpowiednio punkty \(D\) i \(E\), że zachodzi równość \(|CD|=|CE|\). Proste \(AB\) i \(DE\) przecinają się w punkcie \(F\) (zobacz rysunek). Wykaż, że \(|\sphericalangle BAC|=|\sphericalangle ABC|-2\cdot|\sphericalangle AFD|\).

Odpowiedź:      

Udowodniono wykorzystując własności kątów i trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego i wprowadzenie oznaczeń. Spójrzmy na trójkąt \(DEC\). Jest on na pewno równoramienny, co wynika bezpośrednio z treści zadania. Jeśli więc oznaczymy sobie \(|\sphericalangle CDE|=α\), to także \(|\sphericalangle DEC|=α\) Z własności kątów wierzchołkowych wynika, że w takim razie także \(|\sphericalangle BEF|=α\). Dodatkowo oznaczmy sobie miarę kąta \(\sphericalangle EBF=β\). Krok 2. Wyznaczenie wartości kątów \(ACB\), \(ABC\), \(BAC\) oraz \(AFD\). Korzystając z wiedzy, że w każdym z trójkątów suma miar jest równa \(180°\) możemy zapisać, że: \(|\sphericalangle ACB|=180°-2α\           ,\ |\sphericalangle ABC|=180°-β \text{ (kąty przyległe)}\           ,\ |\sphericalangle BAC|=180°-|\sphericalangle ACB|-|\sphericalangle ABC|=\           ,\ =180°-(180°-2α)-(180°-β)=\           ,\ =180°-180°+2α-180°+β=-180°+2α+β \           ,\ |\sphericalangle AFD|=180°-α-β\) Krok 3. Udowodnienie zależności podanej w treści zadania. W drugim kroku obliczyliśmy sobie wartości każdego z potrzebnych kątów, zatem podstawmy te dane do równania z treści zadania i sprawdźmy, czy jest ono rzeczywiście prawdziwe. $$|\sphericalangle BAC|=|\sphericalangle ABC|-2\cdot|\sphericalangle AFD| \           ,\ -180°+2α+β=180°-β-2\cdot(180°-α-β) \           ,\ -180°+2α+β=180°-β-(360°-2α-2β) \           ,\ -180°+2α+β=180°-β-360°+2α+2β \           ,\ -180°+2α+β=-180°+2α+β \           ,\ L=P$$ Równość jest prawdziwa, co kończy nasz dowód.

Teoria:      
W trakcie opracowania