Pracownik ochrony chodzi wzdłuż ogrodzenia parkingu (w kształcie trapezu prostokątnego) ze stałą prędkością \(1\frac{m}{s}\). Obchód zaczyna od wartowni \(A\). Na rysunku przedstawiono plan jego trasy, a obok podano wymiary parkingu.





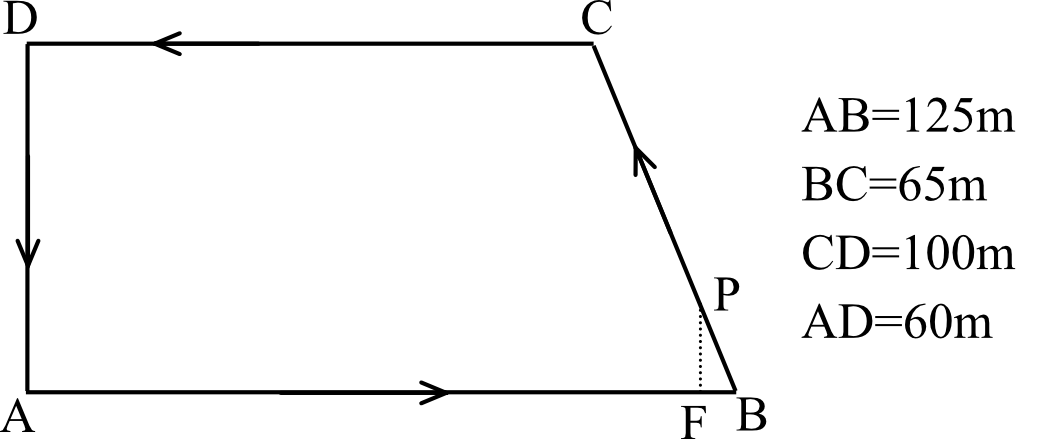
Minęło \(10\) minut od chwili rozpoczęcia obchodu. Na którym odcinku znajduje się pracownik ochrony?

Odpowiedź:      

Ochroniarz znajdzie się na odcinku \(CD\).

Rozwiązanie:      
Krok 1. Obliczenie drogi przebytej w ciągu \(10\) minut. \(10\) minut to jest \(10\cdot60s=600s\). Jeżeli ochroniarz porusza się z prędkością \(1\frac{m}{s}\), to w ciągu \(10\) minut pokona on dystans: $$600s\cdot1\frac{m}{s}=600m$$ Krok 2. Obliczenie długości obwodu trapezu. Znamy wszystkie miary długości boków trapezu, więc bez problemu możemy obliczyć jego obwód: $$Obw=125m+65m+100m+60m=350m$$ Krok 3. Ustalenie na którym odcinku znajduje się pracownik ochrony. Nasz pracownik zaczyna trasę w punkcie \(A\). Jeżeli pokona on \(350m\) to zrobi jedno okrążenie i wróci do punktu \(A\). Po przejściu jednego okrążenia zostaje mu do zrobienia: $$600m-350m=250m$$ Musimy teraz ustalić gdzie się zatrzyma, czyli tak naprawdę gdzie wypada dwieściepięćdziesiąty metr tej trasy. Z punktu \(A\) do \(B\) jest \(125m\), więc to musi być za punktem \(B\). Kolejny odcinek (\(BC\)) ma długość \(65m\), co łącznie dałoby nam trasę \(125m+65m=190m\). Ochroniarz musi iść więc jeszcze dalej. Kolejny odcinek to \(CD\) ma on długość \(100m\), co sprawia że to właśnie tutaj wypadnie ten dwieściepięćdziesiąty metr wyprawy (tak mniej więcej w połowie odcinka \(CD\)).

Teoria:      
W trakcie opracowania