Diagram przedstawia procentowy udział powierzchni poszczególnych kontynentów w całkowitej powierzchni lądów. Przyjmij, że lądy na Ziemi zajmują łącznie \(150mln\;km^2\).





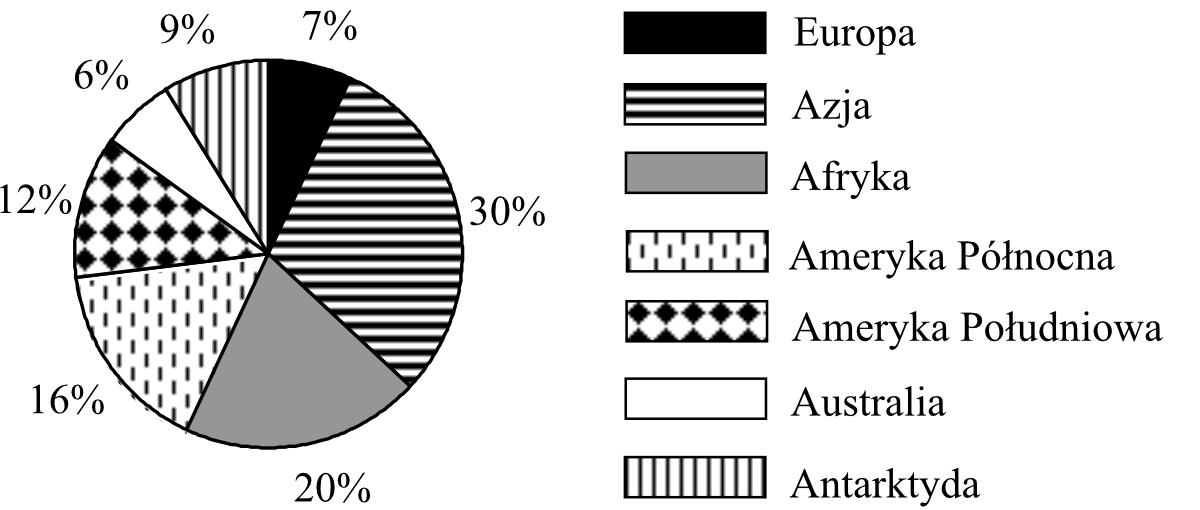
Powierzchnia Antarktydy jest większa od powierzchni Europy o:

A \(3mln\;km^2\)
B \(7,5mln\;km^2\)
C \(30mln\;km^2\)
D \(34,5mln\;km^2\)

Odpowiedź:      

A

Rozwiązanie:      
Zadanie możemy obliczyć na dwa sposoby: I sposób - obliczając powierzchnię dwóch kontynentów: Krok 1. Obliczenie powierzchni Antarktydy. Antarktyda zajmuje \(9\%\) powierzchni Ziemi. Skoro powierzchnia Ziemi jest równa \(150mln\;km^2\), to powierzchnia Antarktydy będzie równa: $$0,09\cdot150mln\;km^2=13,5mln\;km^2$$ Krok 2. Obliczenie powierzchni Europy. Europa zajmuje \(7\%\) powierzchni Ziemi. Skoro powierzchnia Ziemi jest równa \(150mln\;km^2\), to powierzchnia Europy będzie równa: $$0,07\cdot150mln\;km^2=10,5mln\;km^2$$ Krok 3. Obliczenie różnicy powierzchni. Antarktyda jest większa od Europy o: $$13,5mln\;km^2-10,5mln\;km^2=3mln\;km^2$$ II sposób - obliczając różnicę procentową w powierzchni kontynentów: Jeżeli Antarktyda zajmuje \(9\%\) powierzchni Ziemi, a Europa \(7\%\), to znaczy że powierzchnia Antarktydy jest o \(2\) punkty procentowe większa od powierzchni Europy. W związku z tym Antarktyda jest większa od Europy o: $$0,02\cdot150mln\;km^2=3mln\;km^2$$

Teoria:      
W trakcie opracowania