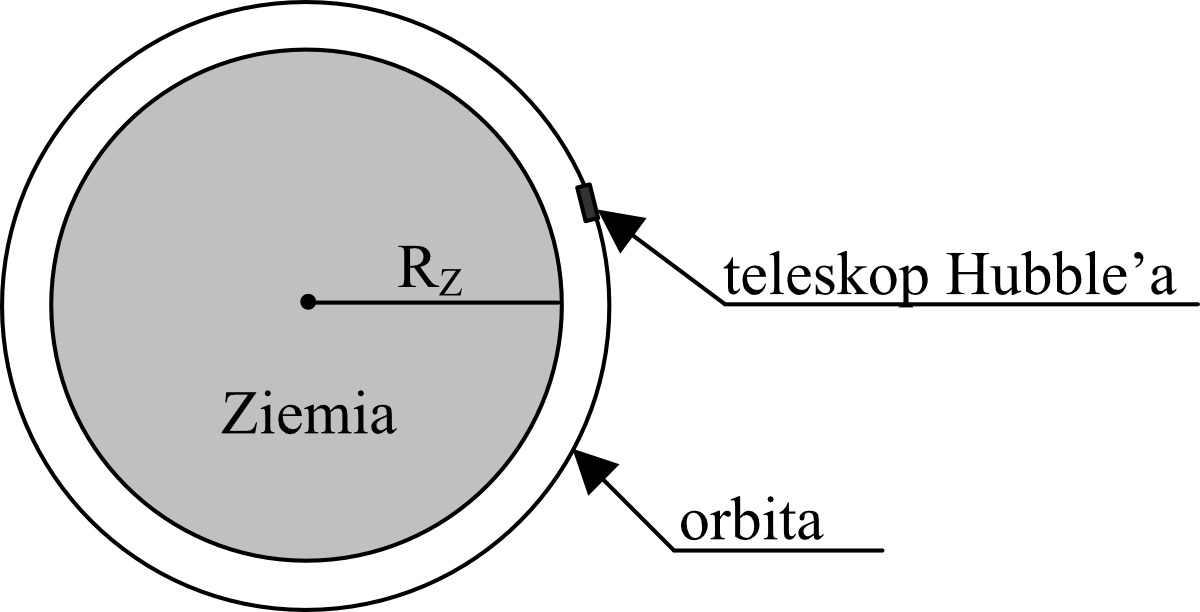
Teleskop Hubble’a znajduje się na orbicie okołoziemskiej na wysokości około \(600km\) nad Ziemią. Oblicz wartość prędkości, z jaką porusza się on wokół Ziemi, jeżeli czas jednego okrążenia Ziemi wynosi około \(100\) minut.

(Przyjmij \(R_{z}=6400km, π=\frac{22}{7}\))

Odpowiedź:      

Teleskop porusza się z prędkością \(v=26400\frac{km}{h}\).

Rozwiązanie:      
Krok 1. Obliczenie promienia okręgu po którym porusza się teleskop. Do obliczenia prędkości (a to jest celem naszego zadania) będziemy potrzebować drogi i czasu. Czas jest podany, musimy więc wyznaczyć drogę. Nasza droga (czyli orbita) jest tak naprawdę obwodem pewnego okręgu, zatem jej długość możemy wyliczyć ze wzoru: $$Obw=2πr$$ Potrzebujemy więc ustalić najpierw jaka jest ta długość promienia. Nie będzie to \(6400km\), bo to jest jedynie promień Ziemi, a teleskop znajduje się jeszcze wyżej. To oznacza, że do wartości \(R_{z}=6400km\) musimy dodać wysokość na jakiej wzniósł się teleskop, czyli \(600km\). Otrzymamy w ten sposób promień okręgu, który jest naszą orbitą. $$r=6400km+600km=7000km$$ Krok 2. Obliczenie długości okręgu/orbity. Znając promień bez problemu wyznaczymy długość orbity. Od razu też użyjemy przybliżenia liczby \(π\), które jest podane w treści zadania: $$Obw=2π\cdot7000km \           ,\ Obw=14000π\;km \           ,\ Obw=14000\cdot\frac{22}{7}km \           ,\ Obw=44000km$$ Krok 3. Obliczenie prędkości poruszania się teleskopu wokół Ziemi. Prędkość poruszania się teleskopu obliczymy ze wzoru: $$v=\frac{s}{t}$$ Długość drogi obliczyliśmy w poprzednim kroku, czas jest podany w treści zadania, więc bez problemu możemy przystąpić do obliczeń. Co prawda w treści zadania nie mamy podane w jakiej jednostce mamy podać tę prędkość (najłatwiej byłoby ją podać w \(\frac{km}{min}\)), ale spróbujmy ją podać w najbardziej typowej jednostce czyli w \(\frac{km}{h}\). Musimy więc jeszcze zapisać, że: $$100min=1\frac{2}{3}h=\frac{5}{3}h$$ W związku z tym prędkość poruszania się teleskopu jest równa: $$v=\frac{44000km}{\frac{5}{3}h}$$ Kreska ułamkowa jest formą dzielenia, więc aby wybrnąć z tego niewygodnego zapisu najprościej będzie to dzielenie zastąpić tak zwanym mnożeniem przez odwrotność: $$v=44000km\cdot\frac{3}{5}h \           ,\ v=26400\frac{km}{h}$$

Teoria:      
W trakcie opracowania