Uzasadnij, że trójkąty prostokątne \(ABC\) i \(KLM\) przedstawione na rysunku są podobne.

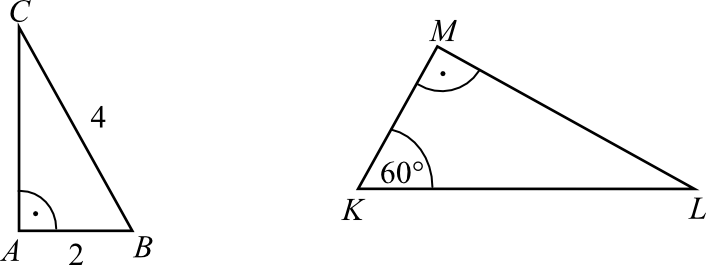
Odpowiedź:      

Udowodniono wykorzystując własności trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Spójrzmy na trójkąt \(ABC\). Wiedząc, że przyprostokątna \(AB\) jest połową przeciwprostokątnej \(BC\) możemy wywnioskować, że nasz trójkąt \(ABC\) jest połową trójkąta równobocznego. W trójkącie równobocznym wszystkie kąty mają miarę \(60°\), zatem \(|\sphericalangle ABC|=60°\). Krok 2. Wyznaczenie miar kątów \(ACB\) oraz \(KLM\) i zakończenie dowodzenia. Skoro suma miar kątów w trójkącie jest równa \(180°\), to: $$|\sphericalangle ACB|=180°-90°-60°=30° \           ,\ |\sphericalangle KLM|=180°-90°-60°=30°$$ W ten sposób udało nam się udowodnić, że obydwa trójkąty mają jednakowe miary kątów (30°, 60°, 90°), zatem są one trójkątami podobnymi na podstawie cechy kąt-kąt-kąt.

Teoria:      
W trakcie opracowania