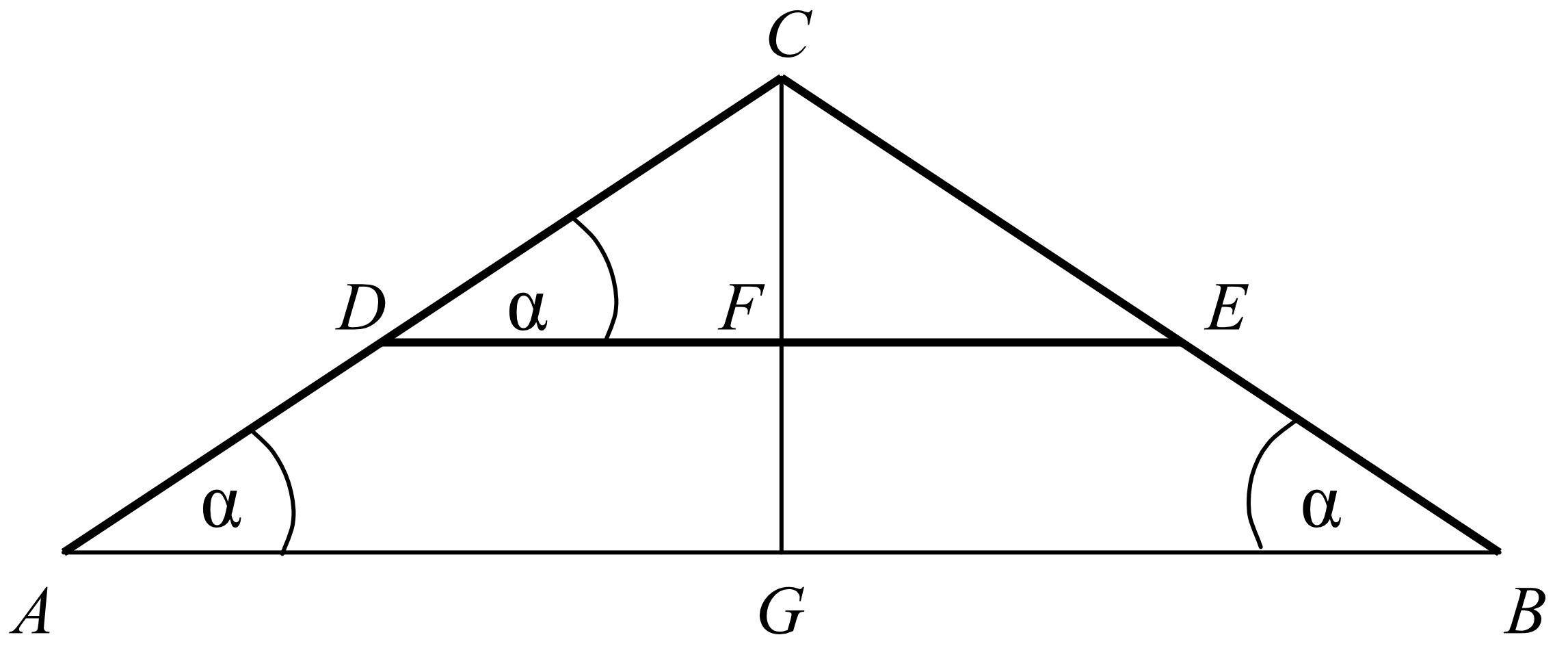
Rysunek przedstawia szkic przekroju dachu dwuspadowego. Wysokość dachu \(GC=5,4m\), a szerokość podstawy \(AB=14,4m\). Oblicz długość krokwi \(AC\) i długość belki \(DE\), wiedząc, że odległość belki od podstawy dachu jest równa \(2,4m\) (czyli \(FG=2,4m)\).

Odpowiedź:      

\(|AC|=9m\) oraz \(|DE|=8m\)

Rozwiązanie:      
Krok 1. Obliczenie długości odcinka \(AC\). Aby obliczyć długość odcinka \(AC\) będziemy musieli posłużyć się Twierdzeniem Pitagorasa i trójkątem \(AGC\). Odcinek \(GC\) jest znany i jego długość wynosi \(5,4m\). Potrzebowalibyśmy poznać długość jeszcze odcinka \(AG\) i ona choć nie jest podana wprost, to jest prosta do wyznaczenia, bowiem będzie to połowa długości odcinka \(AB\). Skoro \(AB\) ma długość \(14,4m\), to odcinek \(AG\) ma długość \(14,4m:2=7,2m\). Zatem: $$(7,2)^2+(5,4)^2=|AC|^2 \           ,\ 51,84+29,16=|AC|^2 \           ,\ |AC|^2=81 \           ,\ |AC|=9[m]$$ Krok 2. Obliczenie długości odcinka \(DE\). Należy zauważyć, że trójkąty \(ABC\) oraz \(DEC\) są podobne (cecha podobieństwa: kąt-kąt-kąt). Skoro tak, to możemy poznać długość boku \(DE\) korzystając z proporcji w stylu: $$\frac{|AC|}{|DC|}=\frac{|AB|}{|DE|} \           ,\ \frac{9}{5}=\frac{14,4}{|DE|}$$ Mnożąc na krzyż otrzymamy: $$9\cdot|DE|=72 \           ,\ |DE|=8[m]$$ To oznacza, że mamy obliczone wszystko co było wymagane - długość krokwi \(AC\) wynosi \(9m\), natomiast długość belki \(DE\) jest równa \(8m\). Uwaga: to nie była jedyna słuszna proporcja którą można zastosować. Równie dobrze można przykładowo zapisać proporcję: $$\frac{AB}{DE}=\frac{CG}{CF}$$ Powyższa proporcja jest także jak najbardziej poprawna proporcja, tylko trzeba dodatkowo obliczyć długość odcinka \(CF\), a będzie ona równa \(5,4-2,4=3\).

Teoria:      
W trakcie opracowania