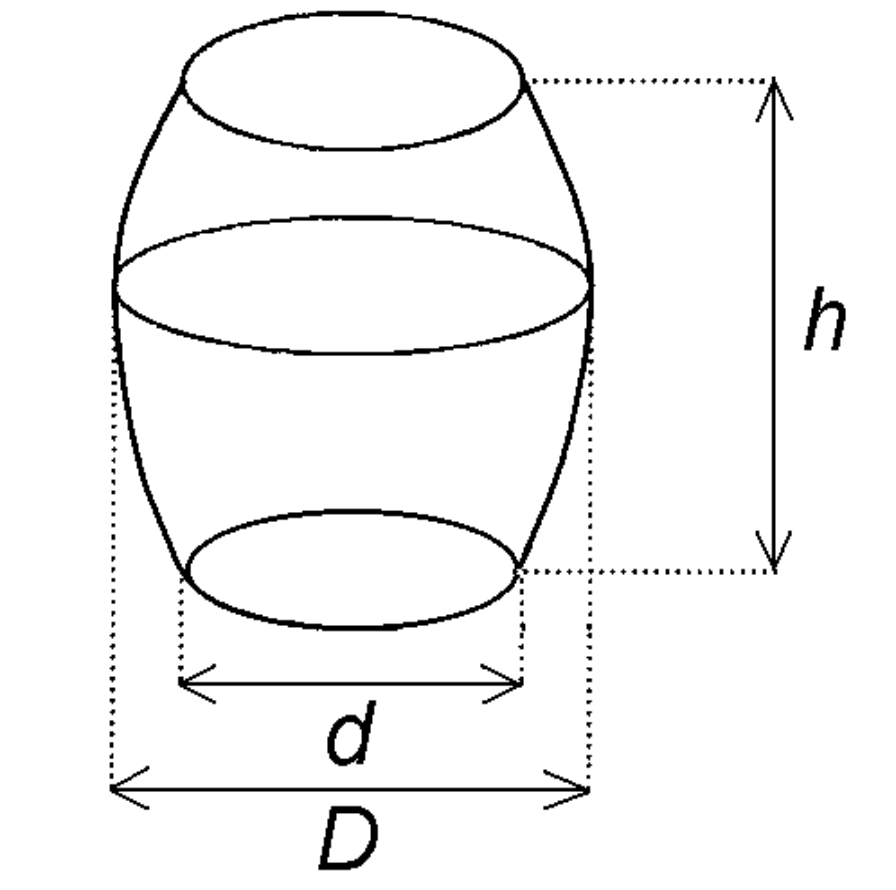
Objętość beczki oblicza się wg wzoru: \(V=\frac{1}{12}\cdot π\cdot(2D^2+d^2)\cdot h\), gdzie:

\(D\) - średnica w miejscu najszerszym

\(d\) - średnica dna

\(h\) - wysokość beczki



Wojtek obmierzył beczkę w ogrodzie. Ma ona wysokość \(12dm\) i średnicę dna równą \(7dm\). Z powodu trudności ze zmierzeniem średnicy w najszerszym miejscu Wojtek zmierzył obwód w najszerszym miejscu. Jest on równy \(33dm\). Oblicz objętość beczki. Dla ułatwienia obliczeń przyjmij \(π=\frac{22}{7}\).

Odpowiedź:      

Objętość beczki wynosi \(V=847dm^3\).

Rozwiązanie:      
Krok 1. Wypisanie danych z treści zadania. Stosując proponowane oznaczenia możemy zapisać, że: \(d=7dm\) \(h=12dm\) \(Obw=33dm\) (obwód beczki w najszerszym miejscu) Przyglądając się wzorowi zapisanemu na początku zadania widzimy, że brakuje nam znajomości długości \(D\), czyli średnicy w miejscu najszerszym. Do jej wyznaczenia wykorzystamy obwód beczki w jej najszerszym miejscu. Krok 2. Obliczenie średnicy w miejscu najszerszym (\(D\)). Wykorzystamy tutaj wzór na obwód okręgu: $$Obw=2πr$$ Podstawiając dane do tego wzoru otrzymamy: $$33dm=2πr \           ,\ r=\frac{33dm}{2π} \           ,\ r=\frac{33dm}{2\cdot\frac{22}{7}} \           ,\ r=\frac{33dm}{\frac{44}{7}} \           ,\ r=33dm\cdot\frac{7}{44} \           ,\ r=5\frac{1}{4}dm$$ To jeszcze nie jest koniec, bo w ten sposób obliczyliśmy promień okręgu (tak naprawdę jest to promień przekroju poprzecznego beczki w jej najszerszym miejscu), a my potrzebujemy znać długość średnicy (czyli naszego \(D\)). Średnica jest dwukrotnie większa od promienia, zatem: $$D=2\cdot r \           ,\ D=2\cdot5\frac{1}{4}dm \           ,\ D=10,5dm$$ Krok 3. Obliczenie objętości beczki. Mamy już wszystkie potrzebne dane, więc możemy bez przeszkód obliczyć objętość naszej beczki, wykorzystując wzór z treści zadania: $$\require{cancel} V=\frac{1}{\cancel{12}}\cdot π\cdot(2\cdot(10,5)^2+(7)^2)\cdot\cancel{12} \           ,\ V=(2\cdot110,25+49)π \           ,\ V=(220,5+49)π \           ,\ V=269,5π \           ,\ V=269,5\cdot\frac{22}{7} \           ,\ V=847[dm^3]$$

Teoria:      
W trakcie opracowania