Dla patrzącego z góry płytka chodnika ma kształt ośmiokąta, w którym kolejne boki są prostopadłe. Na rysunkach przedstawiono jego kształt, sposób układania płytek oraz niektóre wymiary w centymetrach.





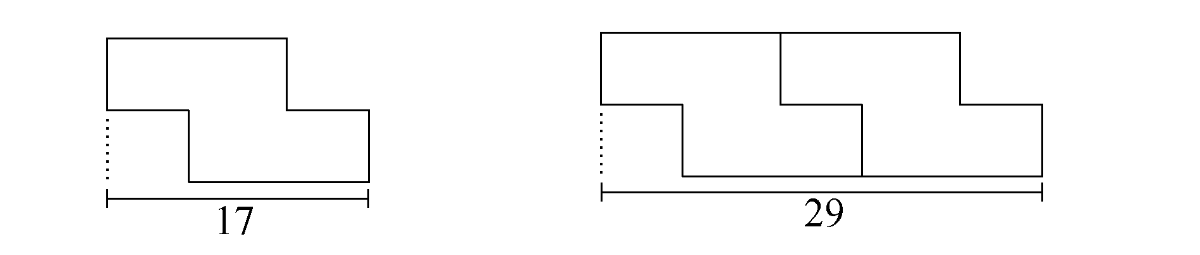
Ułożono sześć płytek.





Oblicz długość odcinka \(a\) oraz napisz wyrażenie algebraiczne, odpowiadające długości analogicznego odcinka dla pasa złożonego z \(n\) płytek.

Odpowiedź:      

\(a=77cm\) oraz \(12n+5\)

Rozwiązanie:      
Krok 1. Obliczenie długości odcinka \(a\). Musimy zauważyć, że dołożenie każdej kolejnej płytki nie zwiększa nam długości chodnika o \(17cm\), bo płytki na siebie zachodzą. Dołożenie każdej kolejnej płytki zwiększa nam długość chodnika o \(29cm-17cm=12cm\). Musimy obliczyć długość \(6\) płytek. Możemy więc to policzyć w taki sposób, że do pierwszej płytki o długości \(17cm\) dodano pięciu kolejnych płytek, z których każda zwiększa długość o \(12cm\). Otrzymamy zatem długość chodnika równą: $$a=17cm+5\cdot12cm=17cm+60cm=77cm$$ Krok 2. Zapisanie wyrażenia algebraicznego. Drugą częścią naszego zadania jest tak naprawdę ustalenie wzoru na długość chodnika. Skorzystamy już z tego co przeanalizowaliśmy sobie w pierwszym kroku, czyli z informacji że długość chodnika jest równa \(17cm\) pierwszej płytki plus \(12cm\) pomnożone przez tyle ile jest dodatkowo dołożonych płytek. Jeśli mamy mieć chodnik składający się z \(n\) płytek, to znaczy że do płytki początkowej trzeba dolożyć jeszcze \(n-1\) dodatkowych płytek, zatem nasz wzór miałby następującą postać: $$17+12(n-1) \           ,\ 17+12n-12 \           ,\ 12n+5$$

Teoria:      
W trakcie opracowania