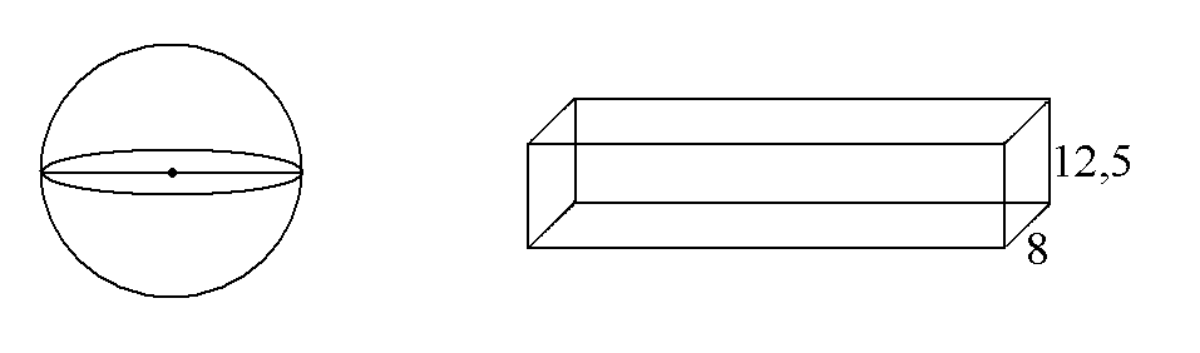
Kula o promieniu \(10cm\) i prostopadłościan, którego jedna ze ścian ma wymiary \(8cm\) i \(12,5cm\), mają taką samą objętość. Oblicz, ile razy pole powierzchni prostopadłościanu jest większe od pola powierzchni kuli. W obliczeniach przyjmij \(π=3\). Wynik zaokrąglij do części dziesiątych.



Użyteczne wzory dotyczące kuli:

\(V=\frac{4}{3}πr^3\)

\(P=4πr^2\)

\(r\) - promień kuli

Odpowiedź:      

Pole powierzchni prostopadłościanu jest nieco ponad \(1,5\) razy większe od pola powierzchni kuli.

Rozwiązanie:      
Krok 1. Obliczenie objętości kuli. Korzystając z danych zawartych w treści zadania oraz przybliżenia \(π=3\) możemy bez przeszkód obliczyć objętość kuli: $$V=\frac{4}{3}πr^3 \           ,\ V=\frac{4}{3}π\cdot10^3 \           ,\ V=\frac{4000}{3}π \           ,\ V=\frac{4000}{3}\cdot3 \           ,\ V=4000[cm^3]$$ Krok 2. Obliczenie brakującej długości krawędzi prostopadłościanu. Do obliczenia pola powierzchni prostopadłościanu brakuje nam długości tej dłuższej krawędzi podstawy. Możemy ją obliczyć korzystając z informacji, że objętość kuli jest równa objętości prostopadłościanu, czyli \(V=4000cm^3\). W związku z tym: $$V=abc \           ,\ 4000=a\cdot8\cdot12,5 \           ,\ 4000=100a \           ,\ a=40[cm]$$ Krok 3. Obliczenie pola powierzchni kuli. Istotą zadania jest policzenie pola powierzchni kuli i prostopadłościanu i porównanie tych dwóch wartości. Zacznijmy od pola powierzchni kuli: $$P_{k}=4πr^2 \           ,\ P_{k}=4π\cdot10^2 \           ,\ P_{k}=400π \           ,\ P_{k}=400\cdot3 \           ,\ P_{k}=1200[cm^2]$$ Krok 4. Obliczenie pola powierzchni prostopadłościanu. W kroku drugim obliczyliśmy brakującą długość krawędzi prostopadłościanu, więc teraz bez przeszkód możemy obliczyć jego pole powierzchni: $$P_{p}=2ab+2ac+2bc \           ,\ P_{p}=2\cdot40\cdot8+2\cdot40\cdot12,5+2\cdot8\cdot12,5 \           ,\ P_{p}=640+1000+200 \           ,\ P_{p}=1840[cm^2]$$ Krok 5. Porównanie pól powierzchni obydwu brył. Musimy jeszcze odpowiedzieć na pytanie ile razy prostopadłościan ma większe pole powierzchni od kuli, zatem: $$\frac{P_{p}}{P_{k}}=\frac{1840}{1200}\approx1,53\approx1,5$$

Teoria:      
W trakcie opracowania