Pojemnik z kremem ma kształt walca o promieniu podstawy \(4cm\) i wysokości \(4,5cm\). Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę o promieniu \(3cm\). Ile razy objętość tej półkuli jest mniejsza od objętości walca?

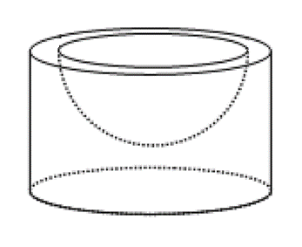
Odpowiedź:      

Objętość półkuli jest czterokrotnie mniejsza od objętości walca.

Rozwiązanie:      
Krok 1. Obliczenie objętości walca. Promień podstawy walca jest równy \(r=4cm\), wysokość wynosi \(h=4,5cm\), zatem objętość walca jest równa: $$V_{w}=πr^2\cdot h \           ,\ V_{w}=π4^2\cdot4,5 \           ,\ V_{w}=16π\cdot4,5 \           ,\ V_{w}=72π[cm^3]$$ Krok 2. Obliczenie objętości półkuli. Oczywiście wzoru jako takiego na objętość półkuli nie mamy, ale znając wzór na objętość kuli \(V_{k}=\frac{4}{3}πr^3\) możemy pomnożyć całość przez \(\frac{1}{2}\) i otrzymamy wtedy objętość półkuli. Z racji tego iż półkula ma promień o długości \(r=3cm\), to jej objętość będzie równa: $$V_{p}=\frac{1}{2}\cdot\frac{4}{3}πr^3 \           ,\ V_{p}=\frac{1}{2}\cdot\frac{4}{3}π\cdot3^3 \           ,\ V_{p}=\frac{1}{2}\cdot\frac{4}{3}π\cdot27 \           ,\ V_{p}=\frac{1}{2}\cdot36π \           ,\ V_{p}=18π[cm^3]$$ Krok 3. Obliczenie stosunku objętości walca do objętości półkuli. Znając obydwie objętości bez problemu możemy odpowiedzieć ile razy objętość półkuli jest mniejsza od objętości walca: $$\frac{V_{w}}{V_{p}}=\frac{72π\;cm^3}{18π\;cm^3}=4$$ To oznacza, że objętość półkuli jest czterokrotnie mniejsza od objętości walca.

Teoria:      
W trakcie opracowania