Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Informator maturalny CKE 2023 Zadanie 31 z 89
Zadanie nr 31. (4pkt)
Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\). Środek \(S\) tego okręgu leży na boku \(AB\) tego trójkąta (zobacz rysunek poniżej). Długości boków \(AB\) i \(AC\) są równe odpowiednio \(|AB|=3r\) oraz \(|AC|=\sqrt{3}r\).
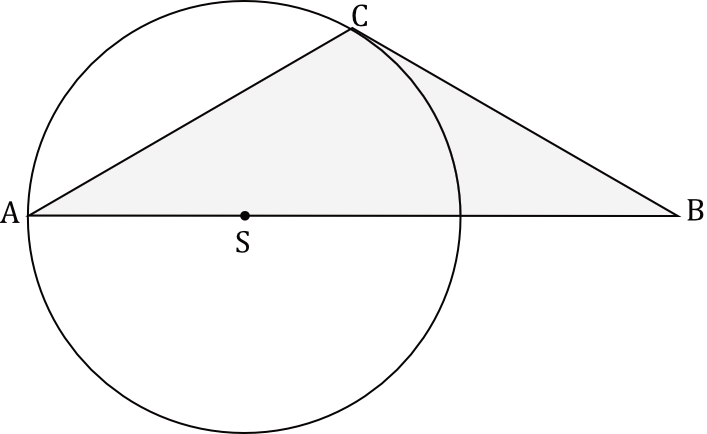
Oblicz miary wszystkich kątów trójkąta \(ABC\).
Odpowiedź:
\(30°, 30°, 120°\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zwróćmy uwagę, że z wierzchołka \(C\) możemy dorysować bok w taki sposób, że otrzymamy trójkąt oparty na średnicy okręgu. Z własności trójkątów wiemy, że taki trójkąt oparty na średnicy będzie zawsze prostokątny i to będzie punkt wyjścia do dalszych obliczeń. Nanosząc dane z treści zadania otrzymamy następujący rysunek szkicowy:
Ustalmy jeszcze skąd wiemy, że odcinek \(DB\) ma długość \(r\). Z treści zadania wynika, że \(|AB|=3r\), a skoro odcinek \(AS\) ma długość \(r\) oraz \(SD\) ma długość \(r\), to odcinek \(DB\) musi mieć \(3r-2r=r\).
Krok 2. Obliczenie długości odcinka \(CD\).
Skoro trójkąt \(ACD\) jest prostokątny, to możemy skorzystać z Twierdzenia Pitagorasa.
$$|AC|^2+|CD|^2=|AD|^2 \ ,\
(\sqrt{3}r)^2+|CD|^2=(2r)^2 \ ,\
3r^2+|CD|^2=4r^2 \ ,\
|CD|^2=r^2 \ ,\
|CD|=r \quad\lor\quad |CD|=-r$$
Ujemną długość oczywiście odrzucamy, zatem \(|CD|=r\).
Krok 3. Dostrzeżenie trójkąta o kątach \(30°, 60°, 90°\).
Powinniśmy zauważyć, że trójkąt \(ADC\) jest trójkątem o kątach \(30°, 60°, 90°\). Wynika to wprost z własności trójkąta, gdyż jedna przyprostokątna ma długość \(r\), a przeciwprostokątna ma \(2r\), czyli jest dwa razy od niej dłuższa. Dodatkowo druga przyprostokątna jest \(\sqrt{3}\) razy większa od pierwszej. To wszystko to cechy charakterystyczne właśnie dla trójkątów o kątach \(30°, 60°, 90°\).
W związku z tym \(|\sphericalangle CAD|=30°\) oraz \(|\sphericalangle ADC|=60°\).
Krok 4. Obliczenie miary kąta \(CDB\).
Spójrzmy na kąt \(CBD\). Jest to kąt przyległy do kąta o mierze \(60°\), a wiemy, że suma miar kątów przyległych jest zawsze równa \(180°\). Skoro tak, to:
$$|\sphericalangle CDB|=180°-60°=120°$$
Krok 5. Obliczenie pozostałych miar kątów trójkąta \(DBC\) oraz \(ABC\).
Wiemy już, że trójkąt \(DBC\) jest trójkątem równoramiennym (ramiona o długości \(r\)). Kąt między tymi ramionami ma miarę \(120°\), a więc na dwa pozostałe kąty zostało nam \(180°-120°=60°\). Kąty przy podstawie \(BC\) będą jednakowej miary (wynika to wprost z własności trójkątów równoramiennych), zatem każdy z nich będzie miał \(60°:2=30°\). Mamy więc następującą sytuację:
Zadanie polega na podaniu miar kątów trójkąta \(ABC\), a więc:
$$|\sphericalangle CAB|=30° \ ,\
|\sphericalangle ABC|=30° \ ,\
|\sphericalangle BCA|=90°+30°=120°$$
Teoria:
W trakcie opracowania
materiał edukacyjny - CKE

