Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Informator maturalny CKE 2023 Zadanie 28 z 86
Zadanie nr 28. (4pkt)
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości \(10m\) (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie \(580\) metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu.
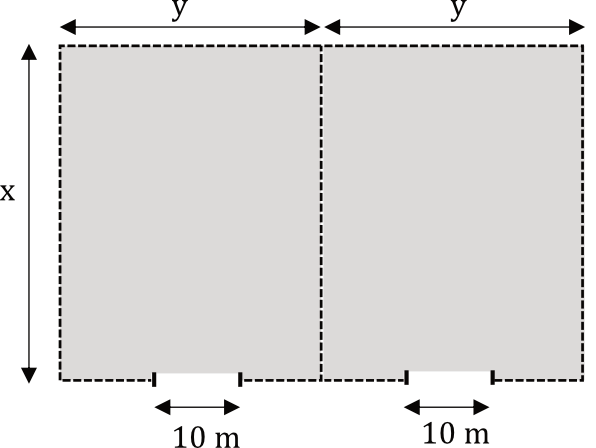
Oblicz wymiary \(x\) i \(y\) każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
Odpowiedź:
\(x=100\) oraz \(y=75\)
Rozwiązanie:
Krok 1. Zapisanie równań.
Wiemy, że długość płotu wynosi \(580m\). Jak spojrzymy na rysunek, to zauważymy, że ten płot musi znaleźć się na trzech odcinkach o długości \(x\) (dwie granice zewnętrzne oraz wewnętrzna) oraz na czterech odcinkach o długości \(y\), które są pomniejszone dwukrotnie o \(10m\). To oznacza, że możemy zapisać następujące równanie:
$$3x+4y-20=580 \ ,\
3x+4y=600$$
Dodatkowo wiemy, że pole powierzchni obliczamy ze wzoru \(P=ab\), co po podstawianiu danych z rysunku możemy zapisać jako:
$$P=x\cdot2y$$
Krok 2. Zapisanie wzoru funkcji \(P(x)\).
Kluczem do sukcesu będzie zapisanie pola powierzchni w postaci funkcji z jedną zmienną, czyli zmienną \(x\). Aby tego dokonać, wyznaczmy wartość \(y\) z równania \(3x+4y=600\).
$$3x+4y=600 \ ,\
4y=600-3x \ ,\
y=150-\frac{3}{4}x$$
Podstawiając teraz \(y=150-\frac{3}{4}x\) do równania \(P=x\cdot2y\) otrzymamy:
$$P=x\cdot2\cdot\left(150-\frac{3}{4}x\right) \ ,\
P=2x\cdot\left(150-\frac{3}{4}x\right) \ ,\
P=300x-\frac{6}{4}x^2 \ ,\
P=-\frac{6}{4}x^2+300x$$
Otrzymaliśmy informację, że pole powierzchni działki można opisać wzorem \(-\frac{6}{4}x^2+300x\). Całość możemy potraktować tak jak funkcję kwadratową (dla jakiejś wartości \(x\) otrzymamy konkretną wartość \(P\)).
Krok 3. Wyznaczenie współrzędnych wierzchołka paraboli.
Wykresem funkcji kwadratowej jest parabola, a tutaj ta parabola będzie mieć ramiona skierowane do dołu (bo współczynnik \(a=-\frac{6}{4}\)). Sytuacja będzie więc wyglądać następująco (zwróć uwagę, że na pionowej osi nie mamy \(y\), tylko pole \(P\)):
Chcemy się dowiedzieć, dla jakiego \(x\) ta pole \(P\) będzie największe, a wiemy, że parabola skierowana ramionami do dołu osiągnie swoją największą wartość w wierzchołku. Obliczmy zatem dla jakiej długości \(x\) ta największa wartość jest przyjmowana, a pomoże nam w tym wzór na współrzędną \(x_{W}\) wierzchołka paraboli:
$$x_{W}=\frac{-b}{2a} \ ,\
x_{W}=\frac{-300}{2\cdot\left(-\frac{6}{4}\right)} \ ,\
x_{W}=\frac{-300}{-3} \ ,\
x_{W}=100$$
Wiemy już, że największa wartość jest przyjmowana, gdy \(x=100\). Gdybyśmy chcieli obliczyć ile wynosi ta największa wartość, to moglibyśmy skorzystać ze wzoru \(q=\frac{-Δ}{4a}\), ale nas to nie interesuje. My musimy poznać wartość \(y\). Skoro tak, to wracamy do równania \(y=150-\frac{3}{4}x\) i podstawiając teraz \(x=100\), otrzymamy:
$$y=150-\frac{3}{4}x \ ,\
y=150-\frac{3}{4}\cdot100 \ ,\
y=150-75 \ ,\
y=75$$
To oznacza, że powierzchnia magazynu będzie największa wtedy, gdy \(x=100\) oraz \(y=75\).
Teoria:
W trakcie opracowania
materiał edukacyjny - CKE

