Spośród nierówności A–D wybierz tę, której zbiór wszystkich rozwiązań zaznaczono na osi liczbowej.

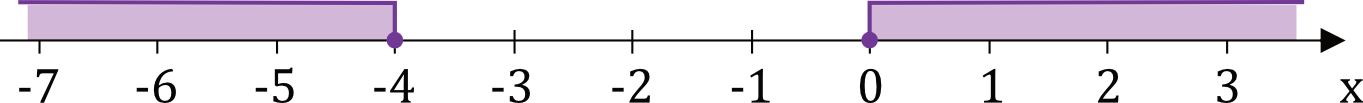
A \(|x+2|\le2\)
B \(|x-2|\le2\)
C \(|x+2|\ge2\)
D \(|x-2|\ge2\)

Odpowiedź:      

C

Rozwiązanie:      
Do tego typu zadań można podchodzić na różne sposoby (w niektórych przypadkach można z samej analizy rysunku wywnioskować poprawną odpowiedź), ale tutaj odpowiedzi są do siebie na tyle podobne, że najprościej i najbezpieczniej będzie po prostu rozwiązać podane nierówności: Odp. A. $$|x+2|\le2 \           ,\ x+2\le2 \quad\land\quad x+2\ge-2 \           ,\ x\le0 \quad\land\quad x\ge-4$$ Odp. B. $$|x-2|\le2 \           ,\ x-2\le2 \quad\land\quad x-2\ge-2 \           ,\ x\le4 \quad\land\quad x\ge0$$ Odp. C. $$|x+2|\ge2 \           ,\ x+2\ge2 \quad\lor\quad x+2\le-2 \           ,\ x\ge0 \quad\lor\quad x\le-4$$ Odp. D. $$|x-2|\ge2 \           ,\ x-2\ge2 \quad\lor\quad x-2\le-2 \           ,\ x\ge4 \quad\lor\quad x\le0$$ Interesujący nas zbiór rozwiązań otrzymaliśmy zatem w trzeciej odpowiedzi.

Teoria:      
W trakcie opracowania