W pewnej grupie \(100\) uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.





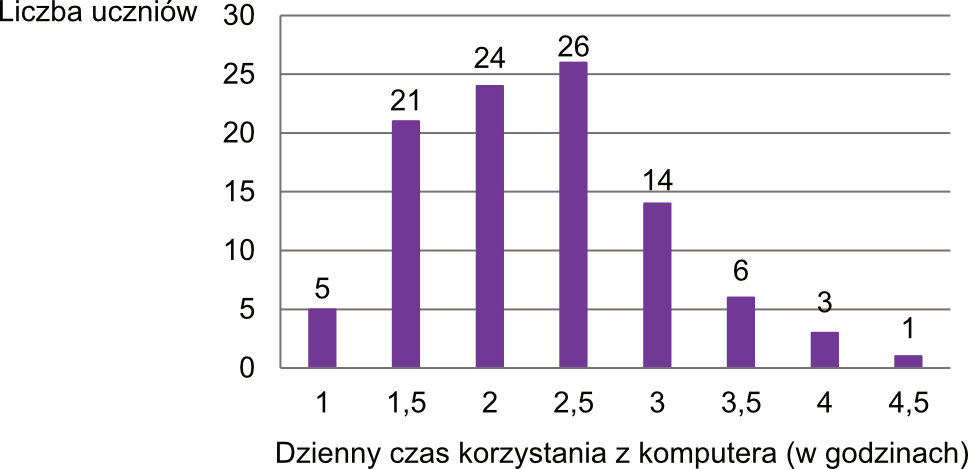
Zadanie 1.

Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.



Mediana dziennego czasu korzystania przez ucznia z komputera jest równa \(2,25\) godziny. P/F

Połowa z tej grupy uczniów korzysta dziennie z komputera przez mniej niż \(2,5\) godziny. P/F



Zadanie 2.

Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa:

A. \(2,25\) godziny

B. \(2,50\) godziny

C. \(2,75\) godziny

D. \(1,50\) godziny

Odpowiedź:      

1. P oraz P
2. B.

Rozwiązanie:      
Zadanie 1. Krok 1. Ocena prawdziwości pierwszego zdania. Z wykresu wynika, że liczba uczniów wynosi: $$5+21+24+26+14+6+3+1=100$$ Liczba uczniów jest parzysta, zatem medianą będzie średnia arytmetyczna dwóch środkowych wyrazów. W tym przypadku środkowymi wyrazami będzie wyraz numer \(50\) i \(51\). Obliczając medianę zawsze musimy mieć uporządkowany ciąg liczb w porządku niemalejącym (czyli od najmniejszej do największej). Oczywiście nie będziemy tutaj wypisywać sobie tego ciągu liczb, tylko analizując wykres, spróbujemy określić który to wyraz jest tym o numerze \(50\) i \(51\). Widzimy, że uczniów korzystających z komputera przez \(1\) lub \(1,5\) lub \(2\) godziny jest łącznie \(5+21+24=50\) osób. To oznacza, że wyraz numer \(50\) jest równy \(2\), a wyraz numer \(51\) jest równy \(2,5\). To oznacza, że mediana będzie równa: $$m=\frac{2+2,5}{2} \           ,\ m=\frac{4,5}{2} \           ,\ m=2,25$$ Pierwsze zdanie jest więc prawdą. Krok 2. Ocena prawdziwości drugiego zdania. Ustaliliśmy już, że w sondażu wzięło udział \(100\) uczniów, z czego \(50\) z nich spędza przed komputerem \(1\) lub \(1,5\) lub \(2\) godziny. To oznacza, że faktycznie połowa uczniów korzysta z komputera mniej niż \(2,5\) godziny, zatem zdanie jest prawdą. Zadanie 2. Dominanta to wynik, który pojawia się najczęściej. Z wykresu wynika jasno, że najczęstszym wskazaniem były \(2,5\) godziny.

Teoria:      
W trakcie opracowania