Dany jest ostrosłup prawidłowy trójkątny \(ABCS\) o podstawie \(ABC\). Punkty \(D\), \(E\) i \(F\) są środkami – odpowiednio – krawędzi bocznych \(AS\), \(BS\) i \(CS\) (zobacz rysunek).





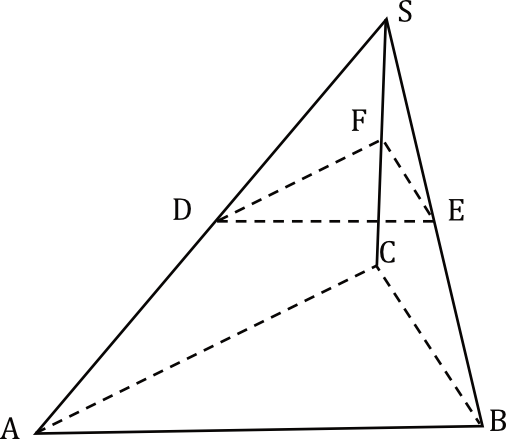
Stosunek objętości ostrosłupa \(DEFS\) do objętości ostrosłupa \(ABCS\) jest równy:

A \(3:4\)
B \(1:4\)
C \(1:8\)
D \(3:8\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie skali podobieństwa. Nasz ostrosłup jest prawidłowy, więc skoro podane punkty \(D\), \(E\) i \(F\) są środkami wskazanych boków, to możemy wywnioskować, że każda krawędź mniejszego ostrosłupa DEFS jest \(2\) razy mniejsza od dużego ostrosłupa \(ABCS\). Jeżeli więc przyjmiemy, że ostrosłup \(ABCS\) jest podstawowy, a \(DEFS\) jest podobny, to skala podobieństwa wynosi \(k=\frac{1}{2}\). Z własności brył podobnych wynika, że gdy przy skali podobieństwa równej \(k\), objętość bryły podobnej stanowi \(k^3\) bryły podstawowej. Jeżeli więc w naszym przypadku objętość bryły \(ABCS\) jest równa \(V\), to objętość bryły \(DEFS\) będzie równa \(k^3\cdot V\), czyli: $$\left(\frac{1}{2}\right)^3\cdot V=\frac{1}{8}V$$ Stosunek objętości ostrosłupa \(DEFS\) do objętości ostrosłupa \(ABCS\) jest zatem równy \(1:8\).

Teoria:      
W trakcie opracowania