Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Przykładowy arkusz CKE 2023 Zadanie 25 z 52
Zadanie nr 25. (1pkt)
Powierzchnię boczną graniastosłupa prawidłowego czworokątnego rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt \(ABCD\), w którym bok \(BC\) odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna AC tego prostokąta ma długość \(16\) i tworzy z bokiem \(BC\) kąt o mierze \(30°\) (zobacz rysunek).
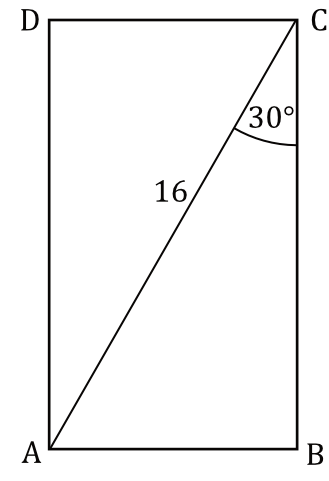
Długość krawędzi podstawy tego graniastosłupa jest równa:
A \(8\)
B \(8\sqrt{3}\)
C \(2\sqrt{3}\)
D \(2\)
Rozwiązanie:
Krok 1. Obliczenie długości odcinka \(AB\).
Spójrzmy na trójkąt \(ABC\). Korzystając z własności trójkątów o kątach \(30°, 60°, 90°\) wiemy, że długość krótszej przyprostokątnej (czyli właśnie boku \(AB\)) będzie dwa razy krótsza od długości przeciwprostokątnej \(AC\). Skoro tak, to:
$$|AB|=16:2 \ ,\
|AB|=8$$
Krok 2. Obliczenie długości krawędzi podstawy tego graniastosłupa.
Musimy zrozumieć, co tak naprawdę policzyliśmy przed chwilą. Prostokąt z treści zadania to rozłożona siatka powierzchni bocznej graniastosłupa (czyli ten prostokąt zawiera w sobie cztery ściany boczne). Bok \(AB\) jest więc tak naprawdę obwodem naszej bryły, a celem zadania jest obliczenie długości krawędzi graniastosłupa. Graniastosłup jest prawidłowy czworokątny, więc ta krawędź będzie cztery razy krótsza od tego boku, czyli:
$$a=8:4 \ ,\
a=2$$
Teoria:
W trakcie opracowania
materiał edukacyjny - CKE

