Firma \(F\) zatrudnia \(160\) osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy \(F\), którzy otrzymują płacę miesięczną w danej wysokości.





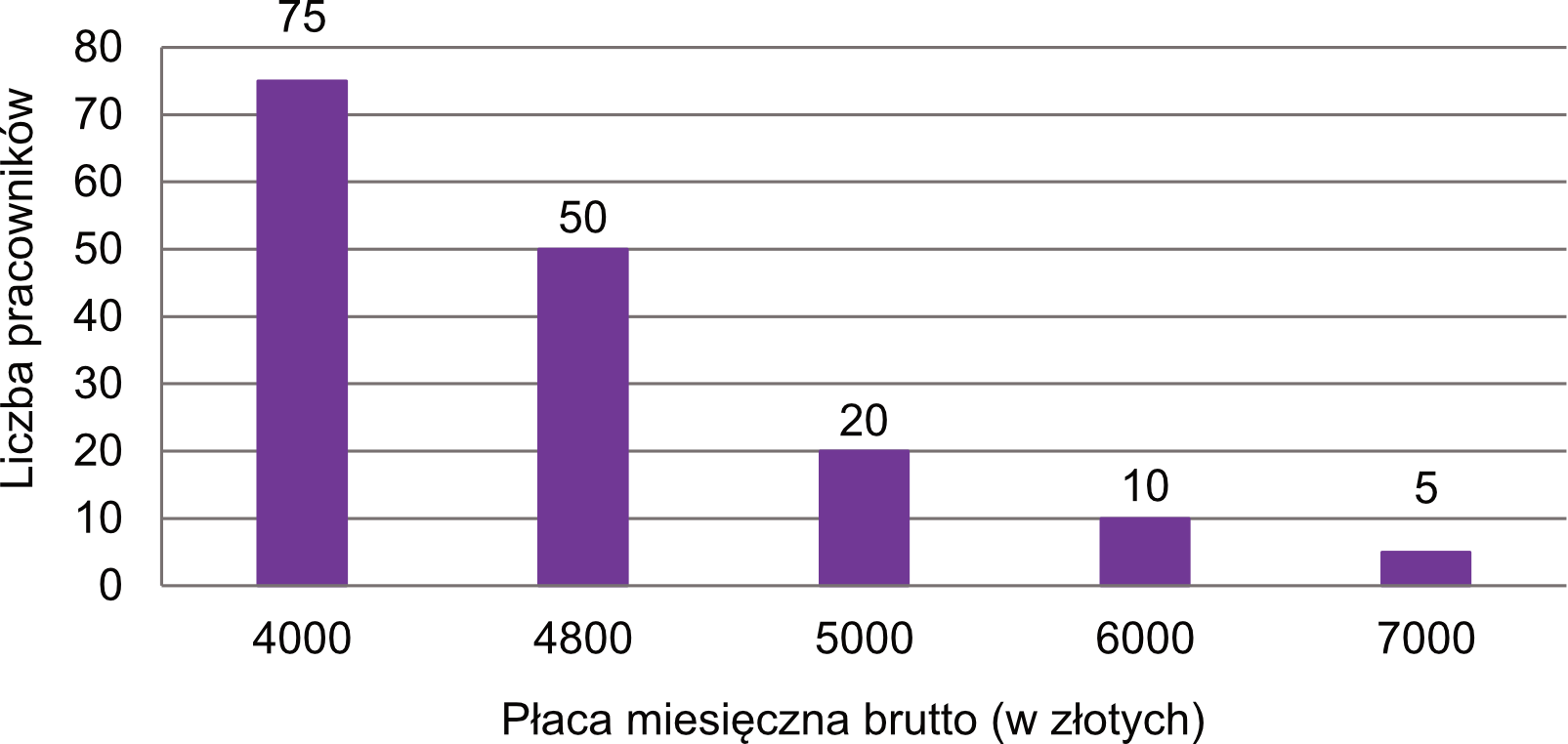
Zadanie 1. Średnia miesięczna płaca brutto w firmie \(F\) jest równa:

A. \(4 593,75 zł\)

B. \(4 800,00 zł\)

C. \(5 360,00 zł\)

D. \(2 399,33 zł\)



Zadanie 2. Mediana miesięcznej płacy pracowników firmy \(F\) jest równa:

A. \(4 000 zł\)

B. \(4 800 zł\)

C. \(5 000 zł\)

D. \(5 500 zł\)



Zadanie 3. Liczba pracowników firmy \(F\), których miesięczna płaca brutto nie przewyższa \(5 000 zł\), stanowi (w zaokrągleniu do \(1\%\)):

A. \(91\%\) liczby wszystkich pracowników tej firmy

B. \(78\%\) liczby wszystkich pracowników tej firmy

C. \(53\%\) liczby wszystkich pracowników tej firmy

D. \(22\%\) liczby wszystkich pracowników tej firmy

Odpowiedź:      

1. A
2. B
3. A

Rozwiązanie:      
Odpowiedź 1. Chcąc obliczyć średnią arytmetyczną, musimy dodać do siebie iloczyny liczby pracowników i ich pensji, a następnie całość podzielić przez liczbę wszystkich zatrudnionych (czyli przez \(160\)). Średnia miesięczna płaca brutto jest więc równa: $$śr=\frac{75\cdot4000+50\cdot4800+20\cdot5000+10\cdot6000+5\cdot7000}{160} \           ,\ śr=\frac{300000+240000+100000+60000+35000}{160} \           ,\ śr=\frac{735000}{160} \           ,\ śr=4 593,75[zł]$$ Odpowiedź 2. Mamy parzystą liczbę pracowników, zatem jeśli uporządkowujemy pensje każdej osoby w ciągu niemalejącym (czyli od najmniejszej do największej) to mediana będzie równa średniej arytmetycznej dwóch środkowych wartości. W tym przypadku mediana będzie średnią zarobków osoby \(80.\) oraz \(81.\) (ponieważ mamy \(160\) pracowników). Z wykresu wynika, że \(75\) osób ma pensję \(4000zł\), a potem \(50\) osób ma pensję \(4800zł\), więc zarobki osoby \(80.\) i \(81.\) wynoszą \(4800zł\). To oznacza, że mediana będzie równa \(4800zł\), co możemy jeszcze rozpisać matematycznie jako: $$m=\frac{4800+4800}{2} \           ,\ m=\frac{9600}{2} \           ,\ m=4800[zł]$$ Odpowiedź 3. Pracowników zarabiających nie więcej niż \(5000zł\) jest łącznie: $$75+50+20=145$$ Skoro wszystkich pracowników jest \(160\), to zarabiający nie więcej niż \(5000zł\) stanowią: $$\frac{145}{160}=0,90625\approx91\%$$

Teoria:      
W trakcie opracowania