W trójkącie \(ABC\) bok \(AB\) ma długość \(4\), a bok \(BC\) ma długość \(4,6\). Dwusieczna kąta \(ABC\) przecina bok \(AC\) w punkcie \(D\) takim, że \(|AD|=3,2\) (zobacz rysunek).





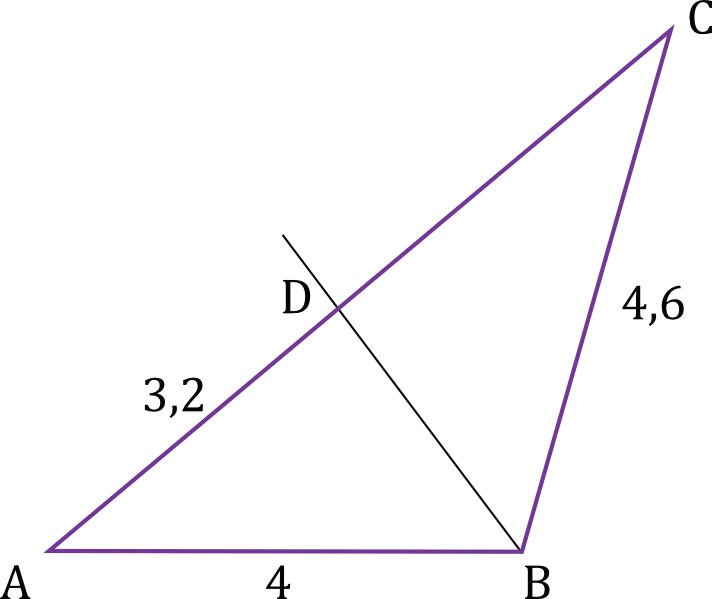
Odcinek \(CD\) ma długość:

A \(\frac{64}{23}\)
B \(\frac{16}{5}\)
C \(\frac{23}{4}\)
D \(\frac{92}{25}\)

Odpowiedź:      

D

Rozwiązanie:      
W zadaniu musimy skorzystać z tak zwanego twierdzenia o dwusiecznej kąta wewnętrznego. Wynika z niego, że dwusieczna kąta dzieli przeciwległy bok proporcjonalnie do długości pozostałych boków. To oznacza, że w naszym przykładzie zachodzi następująca proporcja: $$\frac{|AB|}{|AD|}=\frac{|BC|}{|CD|}$$ Podstawiając dane z rysunku, otrzymamy: $$\frac{4}{3,2}=\frac{4,6}{|CD|}$$ Mnożąc na krzyż, wyjdzie nam, że: $$4\cdot|CD|=3,2\cdot4,6 \           ,\ 4\cdot|CD|=14,72 \           ,\ |CD|=3,68=\frac{92}{25}$$

Teoria:      
W trakcie opracowania