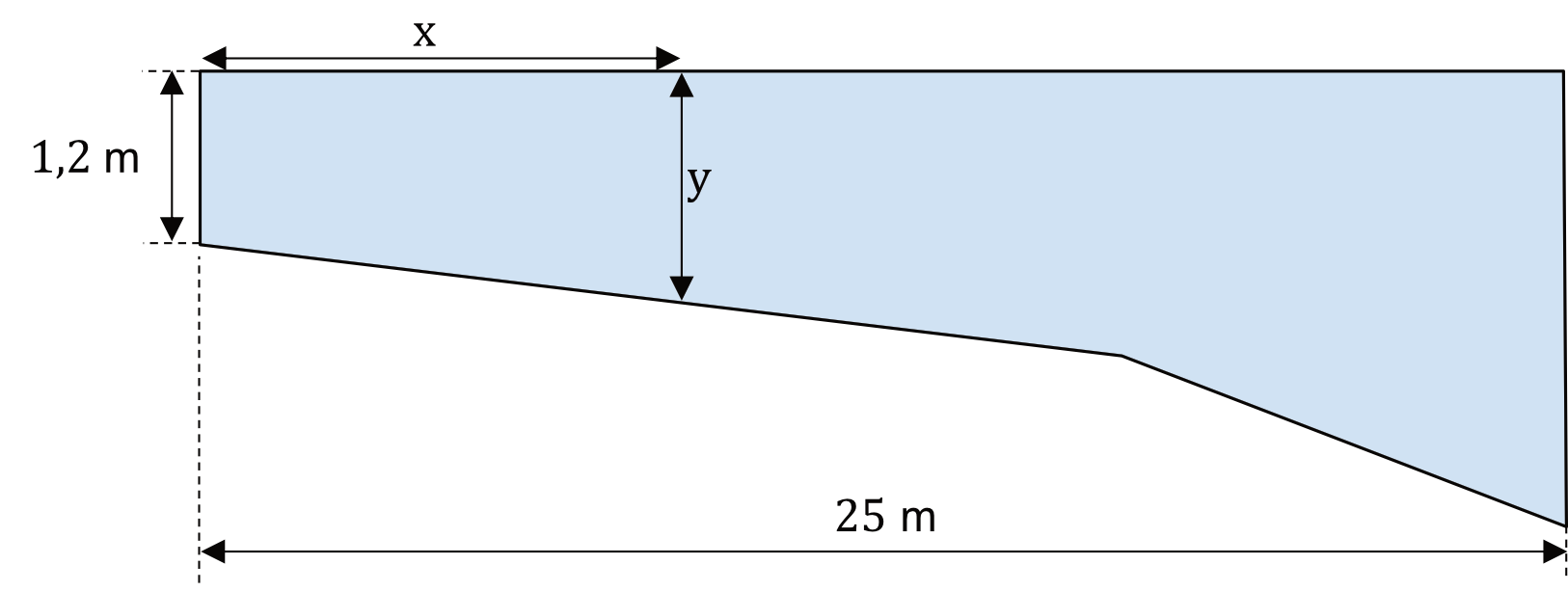
Basen ma długość \(25 m\). W najpłytszym miejscu jego głębokość jest równa \(1,2 m\). Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku.



Głębokość \(y\) basenu zmienia się wraz z odległością \(x\) od brzegu w sposób opisany funkcją:

$$y=\begin{cases} ax+b\quad \text{ dla }\quad 0\le x\le15 m \           ,\

0,18x-0,9\quad \text{ dla }\quad 15 m\le x\le25 m \end{cases}$$



Odległość \(x\) jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości \(x\) i \(y\) są wyrażone w metrach.





Zadanie 1. Największa głębokość basenu jest równa:

A. \(5,4 m\)

B. \(3,6 m\)

C. \(2,2 m\)

D. \(1,8 m\)



Zadanie 2. Oblicz wartość współczynnika \(a\) oraz wartość współczynnika \(b\).

Odpowiedź:      

1. B
2. \(a=\frac{1}{25}\) oraz \(b=1,2\)

Rozwiązanie:      
Odpowiedź 1. Zgodnie z zapisem funkcji, głębokość basenu na długości \(25m\) obliczymy ze wzoru \(y=0,18x-0,9\). Podstawiając zatem \(x=25\), otrzymamy: $$y=0,18x-0,9 \           ,\ y=0,18\cdot25-0,9 \           ,\ y=4,5-0,9 \           ,\ y=3,6[m]$$ To oznacza, że największa głębokość basenu jest równa \(3,6m\). Odpowiedź 2. Z treści zadania wynika, że w najpłytszym miejscu głębokość basenu jest równa \(1,2m\). Czyli moglibyśmy powiedzieć, że dla \(x=0\) ta funkcja przyjmuje wartość \(y=1,2\). Skoro tak, to podstawiając te dane do wzoru \(y=ax+b\), otrzymamy: $$1,2=a\cdot0+b \           ,\ b=1,2$$ To oznacza, że pierwszy wzór z funkcji przybiera postać \(y=ax+1,2\). Musimy jeszcze ustalić wartość współczynnika \(a\). Z całego wzoru wynika, że dla \(x=15\) funkcja może być opisana jednym i drugim wzorem (czyli z jednego i drugiego wzoru wyjdzie nam wtedy ta sama wartość) i to będzie właśnie nasz punkt zaczepienia. Korzystając ze wzoru \(y=0,18x-0,9\), spróbujmy obliczyć głębokość basenu dla \(x=15\): $$y=0,18\cdot15-0,9 \           ,\ y=2,7-0,9 \           ,\ y=1,8$$ Otrzymaną głębokość musimy także otrzymać gdy podstawimy \(x=15\) do wyznaczonej postaci \(y=ax+1,2\), zatem: $$1,8=a\cdot15+1,2 \           ,\ 0,6=15a \           ,\ a=0,04=\frac{1}{25}$$ To oznacza, że \(a=\frac{1}{25}\) oraz \(b=1,2\).

Teoria:      
W trakcie opracowania