Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Egzamin gimnazjalny 2013 - matematyka Zadanie 14 z 9018
Zadanie nr 14. (1pkt)
W równoległoboku \(ABCD\) bok \(AB\) jest dwa razy dłuższy od boku \(AD\). Punkt \(K\) jest środkiem boku \(AB\), a punkt \(L\) jest środkiem boku \(CD\).
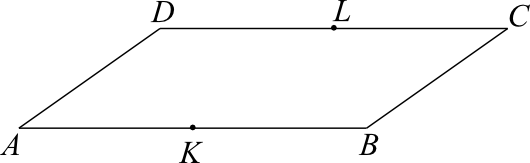
Oceń prawdziwość podanych zdań. Trójkąt \(ABL\) ma takie samo pole, jak trójkąt \(ABD\).
Pole równoległoboku \(ABCD\) jest cztery razy większe od pola trójkąta \(AKD\).
Trójkąt \(ABL\) ma takie samo pole, jak trójkąt \(ABD\).
Odpowiedź:
1) PRAWDA
2) PRAWDA
Rozwiązanie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest prawdą. Do obliczenia pola trójkąta potrzebna jest długość podstawy oraz wysokość (\(P=\frac{1}{2}ah\)). Nie znamy dokładnych miar tych dwóch trójkątów, ale wystarczy zauważyć że obydwa trójkąty mają tą samą podstawę oraz ich wysokość ma tą samą długość. To oznacza, że niezależnie od wartości liczbowych pola jednego i drugiego trójkąta będą dokładnie takie same.
Krok 2. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest prawdą. Zarówno równoległobok jak i trójkąt będą mieć dokładnie tą samą wysokość (opuszczoną z wierzchołka \(D\)). To co je różni to długość podstawy. Jeżeli \(|AK|=\frac{1}{2}|AB|\), to pole trójkąta będzie równe:
$$P_{t}=\frac{1}{2}ah \ ,\
P_{t}=\frac{1}{2}\cdot\frac{1}{2}|AB|\cdot H \ ,\
P_{t}=\frac{1}{4}|AB|\cdot H$$
Pole równoległoboku będzie natomiast równe:
$$P_{r}=|AB|\cdot H$$
Widzimy wyraźnie, że to co różni te dwa wyrażenia to wartość ułamkowa stojąca przy polu trójkąta. To właśnie ona sprawia, że pole równoległoboku niezależnie od dokładnych wymiarów będzie cztery razy większe od pola trójkąta.
Teoria:
W trakcie opracowania
CKE

