Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku \(I\) bączek ma kształt pięciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(5\). Na rysunku \(II\) bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(6\).





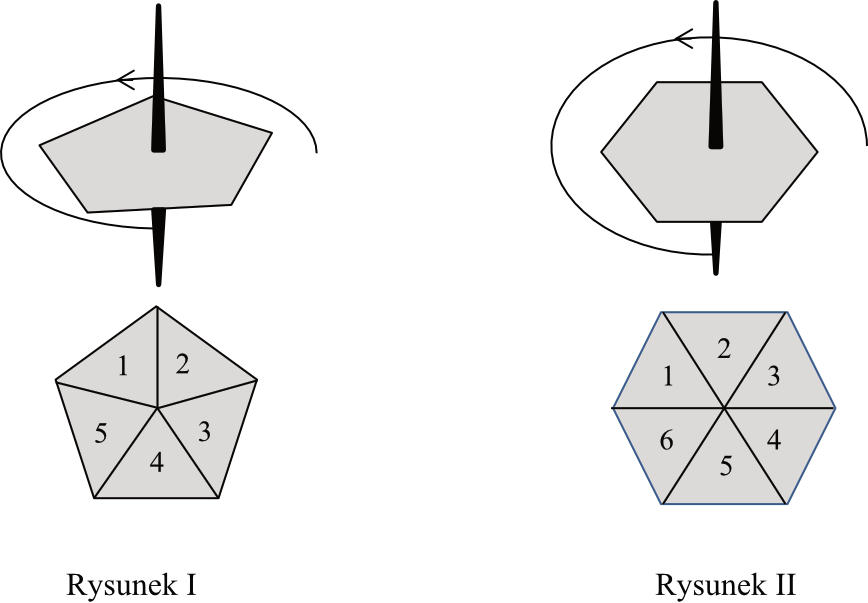
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Prawdopodobieństwo otrzymania liczby większej niż \(3\) na bączku z rysunku \(I\) jest większe niż \(\frac{1}{2}\).
Uzyskanie nieparzystej liczby na bączku z rysunku \(I\) jest tak samo prawdopodobne, jak uzyskanie nieparzystej liczby na bączku z rysunku \(II\).

Prawdopodobieństwo otrzymania liczby większej niż \(3\) na bączku z rysunku \(I\) jest większe niż \(\frac{1}{2}\).

Odpowiedź:      

1) FAŁSZ

2) FAŁSZ

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. Na pierwszym bączku mamy pięć różnych liczb: \(1,2,3,4,5\). Nas interesuje wylosowanie liczby większej niż \(3\), czyli interesują nas dwa wyniki: \(4\) oraz \(5\). Skoro interesują nas dwa wyniki z pięciu możliwych, to prawdopodobieństwo wylosowania liczby większej niż \(3\) jest równe \(\frac{2}{5}\). To oznacza, że to prawdopodobieństwo jest mniejsze niż \(\frac{1}{2}\), czyli pierwsze zdanie jest fałszem. Krok 2. Ocena prawdziwości drugiego zdania. Na pierwszym bączku mamy pięć liczb, a trzy z nich to liczby nieparzyste. W związku z tym prawdopodobieństwo wylosowania liczby nieparzystej jest równe \(\frac{3}{5}\). Na drugim bączku mamy sześć liczb, a trzy z nich to liczby nieparzyste. W związku z tym prawdopodobieństwo wylosowania liczby nieparzystej jest równe \(\frac{3}{6}=\frac{1}{2}\). To oznacza, że prawdopodobieństwa są różne, czyli drugie zdanie jest fałszem.

Teoria:      
W trakcie opracowania