Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne \(T_{1}\) i \(T_{2}\) oraz podano długości ich boków.





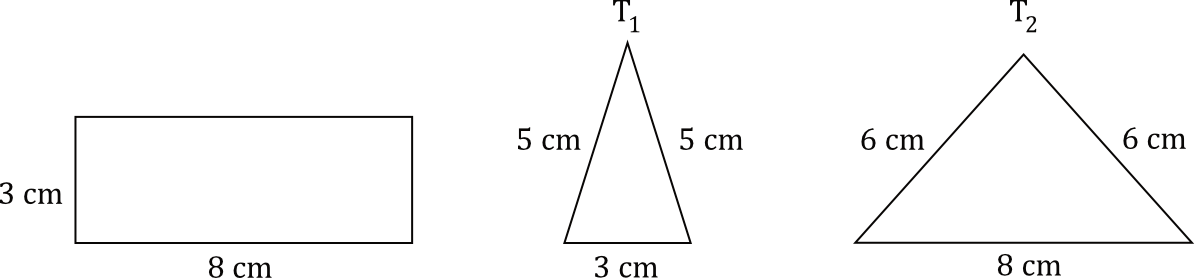
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź A albo B i jej uzasadnienie spośród 1., 2. albo 3. A) długości boków prostokąta są równe długościom podstaw trójkątów \(T_{1}\) i \(T_{2}\).
B) trójkąty \(T_{1}\) i \(T_{2}\) mają podstawy różnej długości.
C) ramiona trójkąta \(T_{1}\) mają inną długość niż ramiona trójkąta \(T_{2}\).

Odpowiedź:      

Nie ponieważ opcja C

Rozwiązanie:      
Aby podane wielokąty mogły być bokami ostrosłupa, to podstawy trójkątów musiałyby być takie same jak boki prostokąta (i ten warunek jest akurat spełniony), a dodatkowo długości ramion tych trójkątów musiałyby mieć pary boków o jednakowej długości (i ten warunek nie został spełniony, przez co siatka graniastosłupa nam się nie domknie). To oznacza, że prawidłową odpowiedzią będzie "Nie, ponieważ ramiona trójkąta \(T_{1}\) mają inną długość niż ramiona trójkąta \(T_{2}\)".

Teoria:      
W trakcie opracowania