Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie \(O\) i boku długości \(8\).





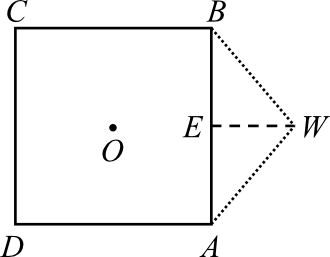
Czy trójkąt \(ABW\) o bokach długości odpowiednio: \(8, 5, 5\) może być ścianą boczną takiego ostrosłupa? A) trójkąt \(ABW\) jest równoramienny
B) odległość \(OE\) jest mniejsza niż wysokość \(EW\) trójkąta \(ABW\)
C) odległość \(OE\) jest większa niż wysokość \(EW\) trójkąta \(ABW\)

Odpowiedź:      

Nie ponieważ opcja C

Rozwiązanie:      
Krok 1. Obliczenie długości \(EW\). Aby obliczyć długość odcinka \(EW\) musimy posłużyć się Twierdzeniem Pitagorasa: $$4^2+|EW|^2=5^2 \           ,\ 16+|EW|^2=25 \           ,\ |EW|^2=9 \           ,\ |EW|=3$$ Krok 2. Obliczenie długości odcinka \(OE\). Odcinek \(OE\) ma długość równą połowie boku kwadratu, czyli \(OE=4\). Krok 3. Interpretacja otrzymanego wyniku. Gdyby kawałek naszej siatki pokazać na rysunku ostrosłupa, to otrzymalibyśmy mniej więcej coś takiego: Spójrzmy na trójkąt prostokątny \(OEW\). W trójkątach prostokątnych najdłuższym bokiem jest zawsze przeciwprostokątna. W tym przypadku, po złożeniu siatki tak się nie stało, bo przeciwprostokątną jest odcinek \(EW=3\), a dolna przyprostokątna ma długość \(OE=4\), co stoi w sprzeczności z zasadami budowy trójkątów prostokątnych. To właśnie ta informacja oznacza, że taki ostrosłup jest po prostu niemożliwy do stworzenia.

Teoria:      
W trakcie opracowania