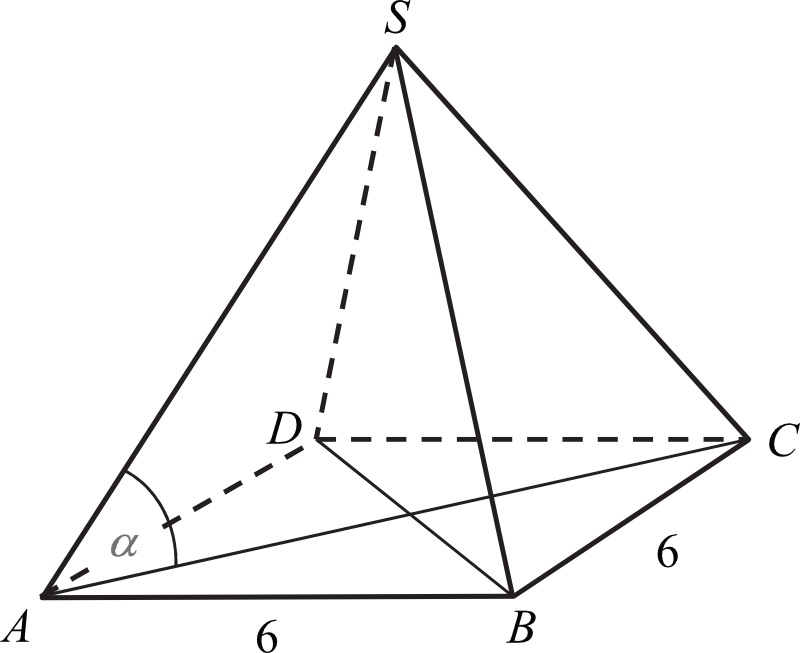
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa \(6\). Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt \(α\) jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta \(α\).

Odpowiedź:      

\(cosα=\frac{\sqrt{5}}{5}\)

Rozwiązanie:      
Krok 1. Obliczenie pola podstawy. W podstawie ostrosłupa mamy kwadrat o boku \(6\), zatem jego pole będzie równe: $$P_{p}=6\cdot6=36$$ Krok 2. Obliczenie pola powierzchni całkowitej. Z treści zadania wynika, że pole powierzchni całkowitej jest cztery razy większe od pola powierzchni podstawy, zatem to pole musi być równe: $$P_{c}=4\cdot P_{p} \           ,\ P_{c}=4\cdot36 \           ,\ P_{c}=144$$ Krok 3. Obliczenie pola pojedynczej ściany bocznej. Skoro pole powierzchni całkowitej jest równe \(144\), a pole podstawy jest równe \(36\), to pole wszystkich czterech ścian bocznych będzie równe: $$P_{b}=P_{c}-P_{p} \           ,\ P_{b}=144-36 \           ,\ P_{b}=108$$ My takich ścian mamy cztery, zatem każda z nich (np. ściana \(BCS\)) ma pole powierzchni równe: $$P_{BCS}=108:4 \           ,\ P_{BCS}=27$$ Krok 4. Obliczenie wysokości ściany bocznej. Spójrzmy na jedną ze ścian bocznych, np. na trójkąt \(BCS\). Jest to trójkąt o podstawie równej \(6\) i polu powierzchni równym \(27\). W związku z tym w prosty sposób możemy wyznaczyć wysokość tego trójkąta: $$P=\frac{1}{2}ah_{b} \           ,\ 27=\frac{1}{2}\cdot6\cdot h_{b} \           ,\ 54=6h_{b} \           ,\ h_{b}=9$$ Krok 5. Obliczenie wysokości ostrosłupa. Spójrzmy na niebieski trójkąt \(SOE\). Odcinek \(OE\) to będzie długość równa połowie krawędzi podstawy, czyli: $$|OE|=6:2 \           ,\ |OE|=3$$ Wiemy też, że \(SE\) ma długość \(9\). Jedynym niewiadomym bokiem w tym trójkącie jest więc odcinek \(SO\), czyli wysokość ostrosłupa. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$H^2+3^2=9^2 \           ,\ H^2+9=81 \           ,\ H^2=72 \           ,\ H=6\sqrt{2}$$ Krok 6. Obliczenie długości krawędzi bocznej. Spójrzmy na trójkąt \(AOS\) i obliczmy długość krawędzi bocznej \(AS\). Odcinek \(AO\) to połowa długości przekątnej podstawy. Skoro mamy kwadrat o boku \(6\), to cała przekątna ma długość \(6\sqrt{2}\), czyli: $$|AO|=6\sqrt{2}:2 \           ,\ |AO|=3\sqrt{2}$$ Odcinek \(SO\) (czyli wysokość trójkąta) jest już nam znana, zatem ponownie korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$(3\sqrt{2})^2+(6\sqrt{2})^2=|AS|^2 \           ,\ 9\cdot2+36\cdot2=|AS|^2 \           ,\ 18+72=|AS|^2 \           ,\ |AS|^2=90 \           ,\ |AS|=\sqrt{90}=3\sqrt{10}$$ Krok 7. Obliczenie cosinusa kąta alfa. Znając długość odcinka \(AO\) oraz \(AS\) bez problemu obliczymy cosinus kąta alfa: $$cosα=\frac{|AO|}{|AS|} \           ,\ cosα=\frac{3\sqrt{2}}{3\sqrt{10}} \           ,\ cosα=\frac{\sqrt{2}}{\sqrt{10}} \           ,\ cosα=\frac{\sqrt{2}}{\sqrt{2}\cdot\sqrt{5}} \           ,\ cosα=\frac{1}{\sqrt{5}} \           ,\ cosα=\frac{1\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} \           ,\ cosα=\frac{\sqrt{5}}{5}$$

Teoria:      
W trakcie opracowania