Podstawą ostrosłupa o wysokości \(H\) jest kwadrat. Na rysunku przedstawiono siatkę i podano długości niektórych krawędzi tego ostrosłupa.





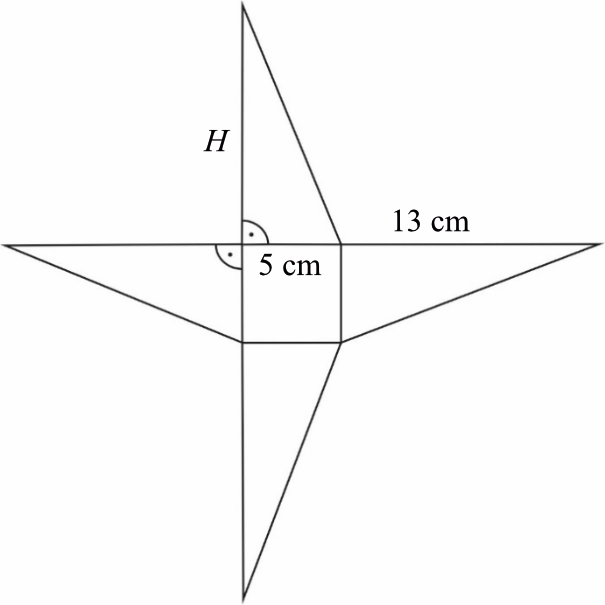
Oblicz objętość tego ostrosłupa.

Odpowiedź:      

\(100cm^3\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zadanie już na samym początku skrywa sporą pułapkę. Wbrew pozorom wysokość górnego trójkąta naszej siatki (czyli jednocześnie wysokość całej bryły) nie będzie mieć długości równej \(13cm\). Długość równą \(13cm\) będzie mieć przeciwprostokątna tego górnego trójkąta prostokątnego, bo tylko wtedy siatka da się złożyć w ostrosłup: Krok 2. Obliczenie wysokości ostrosłupa. Spójrzmy na górny trójkąt prostokątny w naszej siatce. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$5^2+H^2=13^2 \           ,\ 25+h^2=169 \           ,\ H^2=144 \           ,\ H=12 \quad\lor\quad H=-12$$ Ujemny wynik oczywiście odrzucamy, bo wysokość ostrosłupa musi mieć dodatnią długość, zatem zostaje nam \(H=12cm\). Krok 3. Obliczenie pola powierzchni podstawy. W podstawie mamy kwadrat o boku \(5cm\), zatem pole powierzchni podstawy będzie równe: $$P_{p}=a^2 \           ,\ P_{p}=5^2 \           ,\ P_{p}=25[cm^2]$$ Krok 4. Obliczenie objętości ostrosłupa. Znamy już pole podstawy \(P_{p}=25cm^2\), wiemy też że wysokość bryły wynosi \(H=12cm\), zatem objętość będzie równa: $$V=\frac{1}{3}P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot25\cdot12 \           ,\ V=100[cm^3]$$

Teoria:      
W trakcie opracowania