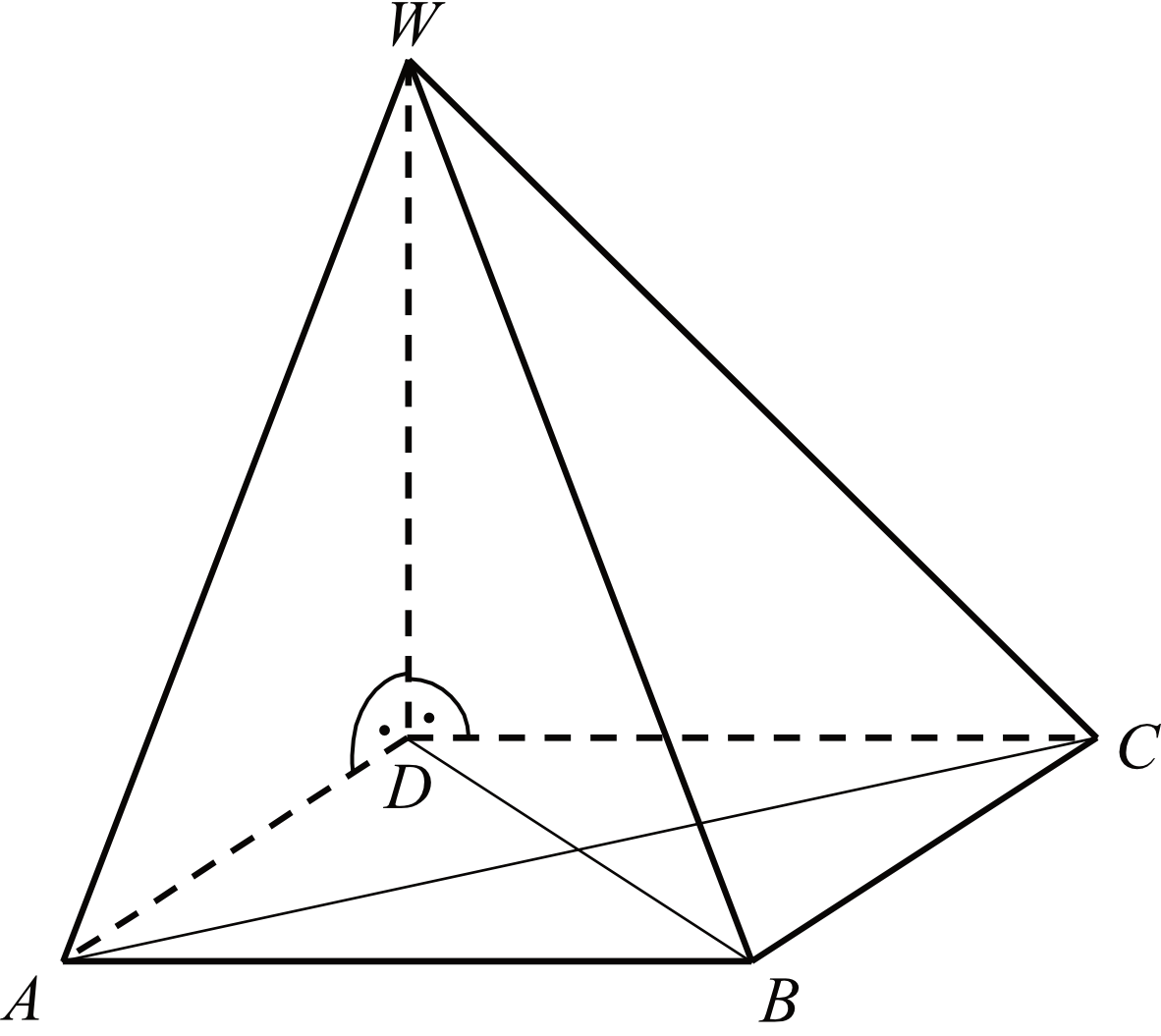
Podstawą ostrosłupa \(ABCDW\) jest prostokąt \(ABCD\). Krawędź boczna \(DW\) jest wysokością tego ostrosłupa. Krawędzie boczne \(AW\), \(BW\) i \(CW\) mają następujące długości: \(|AW|=6\), \(|BW|=9\), \(|CW|=7\). Oblicz objętość tego ostrosłupa.

Odpowiedź:      

\(V=8\sqrt{10}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Zaznaczmy na naszym rysunku długości z treści zadania i przeanalizujmy sobie ten ostrosłup: Potrzebujemy poznać długości wszystkich boków zaznaczonych na zielono, czyli \(x\) oraz \(y\) do obliczenia pola podstawy oraz wysokość \(H\) całego ostrosłupa (którą w naszym przypadku jest odcinek \(DW\)). Krok 2. Wyznaczenie długości odcinka \(BD\). Za chwilę będziemy budować różne równania z Twierdzenia Pitagorasa, ale zanim to nastąpi to jeszcze przydałoby nam się zapisanie wzoru na długość odcinka \(BD\). Zgodnie z Twierdzeniem Pitagorasa: $$x^2+y^2=|BD|^2$$ I w takiej formie możemy to na razie zostawić, bo przy Twierdzeniu Pitagorasa i tak posługujemy się długościami boków podniesionymi do kwadratu. Krok 3. Wypisanie równań na podstawie Twierdzenia Pitagorasa. Z trójkąta \(ADW\) wynika, że: \(y^2+H^2=36\) Z trójkąta \(DCW\) wynika, że: \(x^2+H^2=49\) Z trójkąta \(DBW\) wynika, że: \(|BD|^2+H^2=81\), czyli \(x^2+y^2+H^2=81\) Krok 4. Wyznaczenie poszczególnych długości. Podstawiając z pierwszego równania \(y^2+H^2=36\) do trzeciego równania otrzymamy: $$x^2+36=81 \           ,\ x^2=45 \           ,\ x=\sqrt{45}=\sqrt{9\cdot5}=3\sqrt{5}$$ Podstawiając \(x=\sqrt{45}\) do drugiego równania otrzymamy: $$(\sqrt{45})^2+H^2=49 \           ,\ 45+H^2=49 \           ,\ H^2=4 \           ,\ H=2$$ Podstawiając \(H=2\) do pierwszego równania otrzymamy: $$y^2+2^2=36 \           ,\ y^2+4=36 \           ,\ y^2=32 \           ,\ y=\sqrt{32}=\sqrt{16\cdot2}=4\sqrt{2}$$ Krok 5. Obliczenie pola podstawy. W podstawie znajduje się prostokąt o bokach \(x\) oraz \(y\), zatem: $$P_{p}=x\cdot y \           ,\ P_{p}=3\sqrt{5}\cdot4\sqrt{2} \           ,\ P_{p}=12\sqrt{10}$$ Krok 6. Obliczenie objętości bryły. Znamy wszystkie potrzebne długości, zatem możemy przejść do obliczenia objętości: $$V=\frac{1}{3}P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot12\sqrt{10}\cdot2 \           ,\ V=4\sqrt{10}\cdot2 \           ,\ V=8\sqrt{10}$$

Teoria:      
W trakcie opracowania