Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa \(22\), a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy \(\frac{4\sqrt{6}}{5}\). Oblicz objętość tego ostrosłupa.

Odpowiedź:      

\(V=\frac{3200\sqrt{6}}{3}\)

Rozwiązanie:      
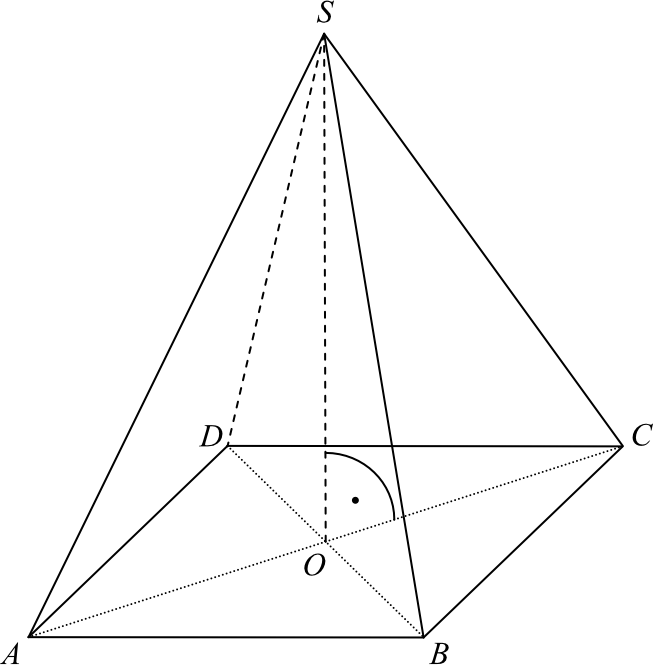
Krok 1. Sporządzenie rysunku poglądowego. Zaznaczmy na rysunku z treści zadania odpowiednie długości, które zostały nam podane w treści. Skoro znamy tangens kąta nachylenia ściany bocznej, to także dorysujemy sobie wysokość naszej bocznej ściany. Już na podstawie tego rysunku warto zauważyć, że jeśli krawędź podstawy oznaczymy sobie jako \(a\), to odcinek \(|OE|=\frac{1}{2}a\). Krok 2. Wyznaczenie wzoru na wysokość ostrosłupa. Korzystając z tangensa spróbujmy wyznaczyć wzór na wysokość ostrosłupa. $$tgα=\frac{|SO|}{|OE|} \           ,\ \frac{4\sqrt{6}}{5}=\frac{H}{\frac{1}{2}a} \quad\bigg/\cdot\frac{1}{2}a \           ,\ H=\frac{4\sqrt{6}}{5}\cdot\frac{1}{2}a \           ,\ H=\frac{2\sqrt{6}}{5}a$$ Krok 3. Wyznaczenie długości krawędzi podstawy (\(a\)). Z Twierdzenia Pitagorasa wiemy, że: $$\left(\frac{1}{2}a\right)^2+H^2=22^2 \           ,\ \left(\frac{1}{2}a\right)^2+\left(\frac{2\sqrt{6}}{5}a\right)^2=22^2 \           ,\ \frac{1}{4}a^2+\frac{4\cdot6}{25}a^2=484 \           ,\ \frac{1}{4}a^2+\frac{24}{25}a^2=484 \           ,\ \frac{25}{100}a^2+\frac{96}{100}a^2=484 \quad\bigg/\cdot100 \           ,\ 25a^2+96a^2=48400 \           ,\ 121a^2=48400 \           ,\ a^2=400 \           ,\ a=20$$ Krok 4. Obliczenie pola podstawy ostrosłupa. Skoro sama podstawa jest kwadratem to jej pole będzie równe: $$P_{p}=a^2 \           ,\ P_{p}=20^2 \           ,\ P_{p}=400$$ Krok 5. Obliczenie długości wysokości ostrosłupa. Podstawiając \(a=20\) do wzoru na wysokość ostrosłupa wyznaczonego w kroku drugim otrzymamy: $$H=\frac{2\sqrt{6}}{5}\cdot20 \           ,\ H=\frac{40\sqrt{6}}{5} \           ,\ H=8\sqrt{6}$$ Krok 6. Obliczenie objętości ostrosłupa. Znając miary wysokości ostrosłupa oraz jego pole podstawy możemy bez problemów obliczyć jego objętość: $$V=\frac{1}{3}\cdot P_{p} \cdot H \           ,\ V=\frac{1}{3}\cdot400\cdot8\sqrt{6} \           ,\ V=\frac{3200\sqrt{6}}{3}$$

Teoria:      
W trakcie opracowania