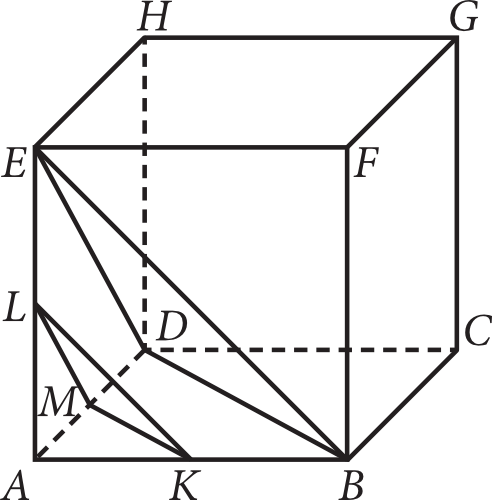
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(10\) (rysunek niżej). Przez środki krawędzi \(AB\), \(AD\) i \(AE\) poprowadzono płaszczyznę \(p\), a przez wierzchołki \(B\), \(D\) i \(E\) − płaszczyznę \(q\) (rys.). Oblicz różnicę wysokości powstałych ostrosłupów o wspólnym wierzchołku \(A\).

Odpowiedź:      

\(\frac{5\sqrt{3}}{3}\)

Rozwiązanie:      
Uwaga: To zadanie jest bardzo nieprecyzyjne. Można odnieść wrażenie, że pytają się nas w zadaniu o to jaka jest różnica między odcinkiem \(AE\) oraz \(AL\), bo są to jak najbardziej wysokości powstałych ostrosłupów, które padają na podstawy \(AKM\) oraz \(ABD\). Zarówno jeden jak i drugi ostrosłup ma wierzchołek w punkcie \(A\), więc wszystko jest zgodne z treścią zadania. Jak tak byśmy podeszli do zadania, to wysokości ostrosłupów są bardzo proste do policzenia, bowiem \(|AE|=10\), a skoro \(L\) jest środkiem odcinka \(AE\) to \(|AL|=5\). Różnica wysokości wyniosłaby więc \(5\). Nieprecyzyjność tego zadania wynika z tego, że intencją autora było to, że wierzchołek \(A\) uznano za "górny wierzchołek", czyli że te dwa ostrosłupy powinny być obrócone w taki sposób, że w podstawie pierwszego znajduje się trójkąt \(MKL\), a w podstawie drugiego znajduje się trójkąt \(BDE\). Wtedy wysokość poprowadzona z wierzchołka \(A\) padałaby na te dwie płaszczyzny. Krok 1. Sporządzenie rysunku pomocniczego. Jedną z głównych trudności w tym zadaniu jest prawidłowe odszukanie poszukiwanych ostrosłupów (o czym wspomniałem powyżej). Narysujmy więc sobie te dwa ostrosłupy oddzielnie i zróbmy to od razu tak, jak zazwyczaj rysujemy ostrosłupy (czyli podstawy \(MKL\) oraz \(DBE\) na dole, a wierzchołek \(A\) na górze). Krok 2. Obliczenie długości boków \(BD\), \(BE\) oraz \(DE\). Jak spojrzymy się na rysunek z treści zadania to możemy zauważyć, że boki \(BD\), \(BE\) oraz \(DE\) są przekątnymi kwadratów, które znalazły się w podstawie lub ścianie bocznej sześcianu. Z własności kwadratów wiemy, że przekątne kwadratów o boku \(a\) mają długość \(a\sqrt{2}\). Skoro więc krawędź kwadratu ma długość \(10\), to wszystkie te trzy boki będą miały długość \(10\sqrt{2}\). Krok 3. Obliczenie wysokości dużego ostrosłupa. Zacznijmy od policzenia wysokości dużego ostrosłupa. Tutaj też możemy sporządzić prosty rysunek, zaznaczając przy okazji trójkąt prostokątny z którego obliczymy poszukiwaną wysokość: Widzimy wyraźnie, że dolna przyprostokątna naszego trójkąta prostokątnego ma długość \(\frac{2}{3}\) wysokości trójkąta równobocznego, który znalazł się w podstawie. Wysokość takich trójkątów obliczamy ze wzoru \(h=\frac{a\sqrt{3}}{2}\), zatem: $$BP=\frac{2}{3}h_{p} \           ,\ BP=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2} \           ,\ BP=\frac{2}{3}\cdot\frac{10\sqrt{2}\sqrt{3}}{2} \           ,\ BP=\frac{10\sqrt{6}}{3}$$ Teraz znając dwie długości boków w trójkącie prostokątnym \(BPA\) możemy bez problemu obliczyć poszukiwaną wysokość z Twierdzenia Pitagorasa: $$\left(\frac{10\sqrt{6}}{3}\right)^2+H^2=10^2 \           ,\ \frac{100\cdot6}{9}+H^2=100 \           ,\ \frac{600}{9}+H^2=\frac{900}{9} \           ,\ H^2=\frac{300}{9} \           ,\ H^2=\frac{100}{3} \           ,\ H=\sqrt{\frac{100}{3}} \quad\lor\quad H=-\sqrt{\frac{100}{3}}$$ Ujemny wynik oczywiście odrzucamy, bo wysokość nie może być ujemna, zatem zostaje nam \(H=\sqrt{\frac{100}{3}}\), co możemy jeszcze uprościć do następującej postaci: $$H=\sqrt{\frac{100}{3}} \           ,\ H=\frac{10}{\sqrt{3}} \           ,\ H=\frac{10\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \           ,\ H=\frac{10\sqrt{3}}{3}$$ Krok 4. Dostrzeżenie podobieństwa ostrosłupów. Jeżeli spojrzymy na nasze ostrosłupy, które narysowaliśmy sobie w pierwszym kroku, to powinniśmy dostrzec, że są one ostrosłupami podobnymi, bo każdy wymiar drugiego ostrosłupa jest dwukrotnie mniejszy od wymiaru pierwszego ostrosłupa. Jeżeli więc potraktujemy pierwszy ostrosłup jako bryłę podstawową, a drugi jako bryłę podobną, bo możemy zapisać, że skala podobieństwa będzie równa \(k=\frac{1}{2}\). Krok 5. Obliczenie wysokości małego ostrosłupa. Skoro skala podobieństwa tych ostrosłupów jest równa \(k=\frac{1}{2}\), to także wysokość małego ostrosłupa będzie dwukrotnie mniejsza od wysokości ostrosłupa dużego. W związku z tym: $$H_{m}=\frac{1}{2}H \           ,\ H_{m}=\frac{1}{2}\cdot\frac{10\sqrt{3}}{3} \           ,\ H_{m}=\frac{5\sqrt{3}}{3}$$ Krok 6. Obliczenie różnicy między wysokością dużego i małego ostrosłupa. Zgodnie z treścią zadania musimy jeszcze obliczyć różnicę wysokości dwóch ostrosłupów, zatem: $$H-H_{m}=\frac{10\sqrt{3}}{3}-\frac{5\sqrt{3}}{3}=\frac{5\sqrt{3}}{3}$$

Teoria:      
W trakcie opracowania