Dany jest trójkąt \(ABC\) o bokach długości: \(|AB|=4\), \(|BC|=5\), \(|AC|=6\). Na tym trójkącie opisano okrąg o środku w punkcie \(S\) i promieniu \(R\).





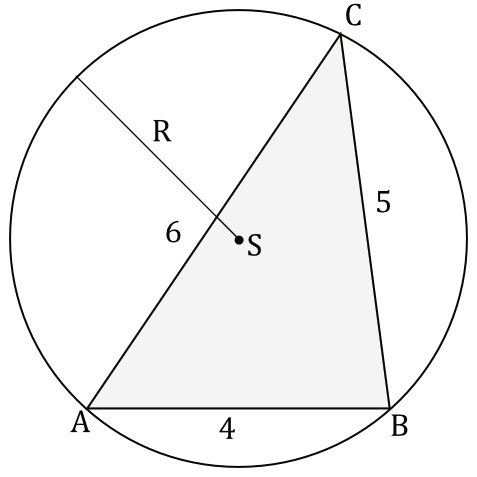
Oblicz promień \(R\) okręgu opisanego na trójkącie \(ABC\).

Odpowiedź:      

\(R=\frac{8\sqrt{7}}{7}\)

Rozwiązanie:      
Krok 1. Wyznaczenie wartości \(cos\alpha\). Chcielibyśmy na pewno skorzystać z twierdzenia sinusów, ale nie znamy miary żadnego z kątów, przez co nie mamy dobrego punktu zaczepienia. Możemy jednak poznać miarę takiego kąta, korzystając z twierdzenia cosinusów. Jeżeli oznaczymy sobie kąt przy wierzchołku \(A\) jako \(\alpha\), to zgodnie z twierdzeniem cosinusów będziemy mogli zapisać, że: $$|BC|^2=|AC|^2+|AB|^2-2\cdot|AC|\cdot|AB|\cdot cos\alpha$$ Podstawiając dane z treści zadania, otrzymamy: $$5^2=6^2+4^2-2\cdot6\cdot4\cdot cos\alpha \           ,\ 25=36+16-48\cdot cos\alpha \           ,\ 25=52-48\cdot cos\alpha \           ,\ -27=-48\cdot cos\alpha \           ,\ cos\alpha=\frac{27}{48}=\frac{9}{16}$$ Krok 2. Wyznaczenie wartości \(sin\alpha\). Korzystając z jedynki trygonometrycznej możemy teraz zapisać, że: $$sin^2\alpha+cos^2\alpha=1 \           ,\ sin^2\alpha+\left(\frac{9}{16}\right)^2=1 \           ,\ sin^2\alpha+\frac{81}{256}=1 \           ,\ sin^2\alpha=\frac{175}{256} \           ,\ sin\alpha=\sqrt{\frac{175}{256}} \quad\lor\quad sin\alpha=-\sqrt{\frac{175}{256}}$$ Nasz kąt \(\alpha\) jest kątem ostrym, a dla takich kątów sinus przyjmuje jedynie dodatnie wartości. Stąd też zostaje nam jedynie \(sin\alpha=\sqrt{\frac{175}{256}}\), co możemy jeszcze rozpisać jako: $$sin\alpha=\sqrt{\frac{175}{256}}=\frac{\sqrt{25\cdot7}}{16}=\frac{5\sqrt{7}}{16}$$ Krok 3. Obliczenie długości promienia \(R\). Teraz możemy przystąpić do działania, które planowaliśmy od samego początku, czyli do wykorzystania twierdzenia sinusów. Możemy zapisać, że: $$\frac{|BC|}{sin\alpha}=2R \           ,\ \frac{5}{\frac{5\sqrt{7}}{16}}=2R \           ,\ 2R=5\cdot\frac{16}{5\sqrt{7}} \           ,\ 2R=\frac{16}{\sqrt{7}} \           ,\ R=\frac{8}{\sqrt{7}} \           ,\ R=\frac{8\cdot\sqrt{7}}{\sqrt{7}\cdot\sqrt{7}} \           ,\ R=\frac{8\sqrt{7}}{7}$$

Teoria:      
W trakcie opracowania