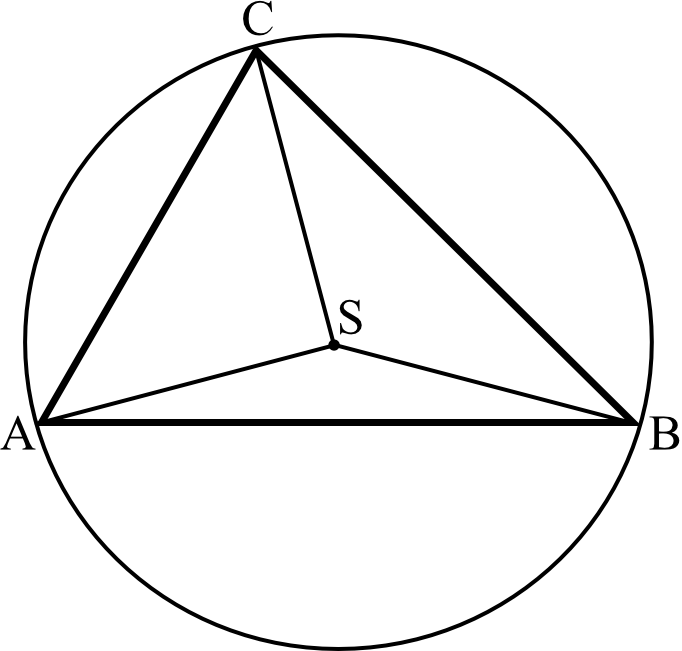
Punkt \(S\) jest środkiem okręgu opisanego na trójkącie ostrokątnym \(ABC\). Kąt \(ACS\) jest trzy razy większy od kąta \(BAS\), a kąt \(CBS\) jest dwa razy większy od kąta \(BAS\). Oblicz kąty trójkąta \(ABC\).

Odpowiedź:      

\(|\sphericalangle ABC|=45°, |\sphericalangle BCA|=75°, |\sphericalangle CAB|=60°\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Musimy dostrzec, że trójkąty \(ABS\), \(BSC\) i \(ASC\) są równoramienne, bo każdy z nich ma dwa ramiona o długości promienia okręgu. Trójkąty równoramienne mają tę cechę, że przy podstawie posiadają dwa kąty identycznej miary. W związku z tym, jeśli oznaczymy sobie jako \(α\) kąt \(BAS\), to także kąt \(ABS\) jest równy \(α\). Z treści zadania wiemy też, że kąt \(CBS\) jest dwa razy większy od kąta \(BAS\), czyli zgodnie z naszymi oznaczeniami miara kąta \(CBS\) jest równa \(2α\). To oznacza, że i kąt \(BCS\) ma miarę \(2α\). I analogicznie skoro kąt \(ACS\) jest równy \(3α\), to i kąt \(CAS\) ma miarę \(3a\). Oznaczmy sobie wszystkie te dane na rysunku pomocniczym. Krok 2. Obliczenie miar kątów trójkąta \(ABC\). Suma kątów w trójkącie jest równa \(180°\). Na rysunku widzimy, że: $$|\sphericalangle ABC|+|\sphericalangle BCA|+|\sphericalangle CAB|=3α+5α+4α=12α$$ To oznacza, że bardzo łatwo możemy wyznaczyć wartość \(α\) i tym samym obliczyć miarę każdego z kątów. $$12α=180° \           ,\ α=15°$$ Zatem: $$|\sphericalangle ABC|=3α=3\cdot15°=45° \           ,\ |\sphericalangle BCA|=5α=5\cdot15°=75° \           ,\ |\sphericalangle CAB|=4α=4\cdot15°=60°$$

Teoria:      
W trakcie opracowania