Środek \(S\) okręgu opisanego na trójkącie równoramiennym \(ABC\), o ramionach \(AC\) i \(BC\), leży wewnątrz tego trójkąta (zobacz rysunek).







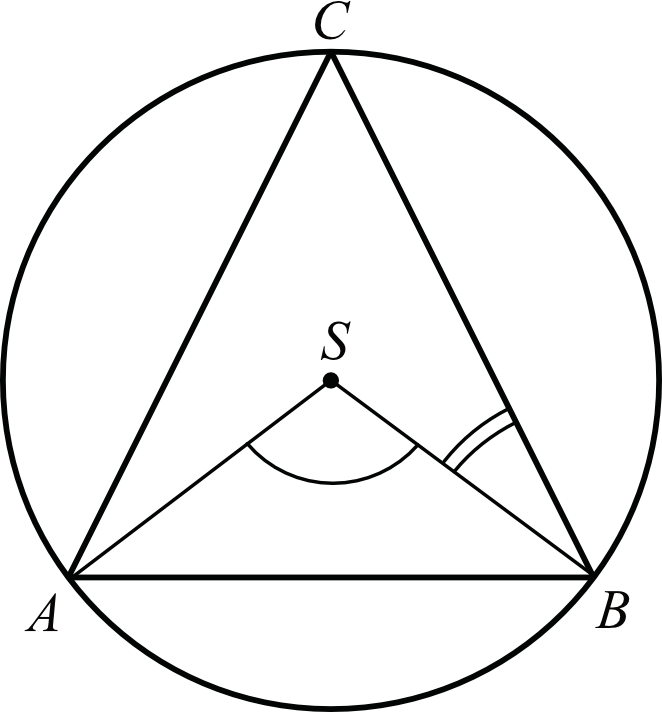
Wykaż, że miara kąta wypukłego \(ASB\) jest cztery razy większa od miary kąta wypukłego \(SBC\).

Odpowiedź:      

Udowodniono wykorzystując własności trójkątów równoramiennych i przystających.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Zadanie jest najprostsze do udowodnienia w momencie, gdy dorysujemy sobie odcinek pomocniczy \(CS\). Powstaną nam w tym momencie dwa trójkąty \(ASC\) oraz \(SBC\), o których wiemy że są równoramienne i przystające. Skąd to wiemy? Ramiona tych dwóch trójkątów mają długość równą promieniowi koła, więc z tego faktu możemy wysnuć wniosek, że są to trójkąty równoramienne. O tym, że są przystające wiemy dzięki temu, że w treści zadania podano nam informację, że boki \(AC\) oraz \(BC\) są równej miary - czyli obydwa te trójkąty mają ramiona równej długości i mają tą samą długość podstawy. To z kolei pozwoli nam wysnuć wniosek, że jeżeli kąt \(SBC\) oznaczymy jako \(α\), to także kąty \(SCB\), \(SAC\) oraz \(SCA\) będą miały miarę równą \(α\) (wiemy to, bo kąty równoramienne mają identyczne miary kątów przy swojej podstawie). Wszystkie ewentualne wątpliwości rozwieje poniższy rysunek. Krok 2. Wyznaczenie miary kątów \(ASC\) oraz \(BSC\). Skoro już ustaliliśmy, że trójkąty \(ASC\) oraz \(SBC\) mają po dwa kąty o mierze równej \(α\), to i trzeci kąt jesteśmy w stanie obliczyć i będzie to \(180°-2α\). W związku z tym: $$|\sphericalangle ASC|=180°-2α \           ,\ |\sphericalangle BSC|=180°-2α$$ Krok 3. Wyznaczenie miary kąta \(ASB\). Znając miary kątów wyliczone w drugim kroku możemy teraz obliczyć miarę kąta \(ASB\): $$|\sphericalangle ASB|=360°-|\sphericalangle ASC|-|\sphericalangle BSC| \           ,\ |\sphericalangle ASB|=360°-(180°-2α)-(180°-2α) \           ,\ |\sphericalangle ASB|=360°-180°+2α-180°+2α \           ,\ |\sphericalangle ASB|=4α$$ W ten oto sposób udowodniliśmy, że miara kąta \(ASB\) jest czterokrotnie większa od miary kąta \(SBC\).

Teoria:      
W trakcie opracowania