Czas \(T\) połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę - tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder \(N(t)\) izotopu promieniotwórczego pozostających w próbce po czasie \(t\), licząc od chwili \(t_{0}=0\), wyraża się zależnością wykładniczą:

$$N(t)=N_{0}\left(\frac{1}{2}\right)^{\frac{t}{T}}$$



gdzie \(N_{0}\) jest liczbą jąder izotopu promieniotwórczego w chwili początkowej \(t_{0}=0\).



Zadanie 1.

Na poniższych rysunkach 1.-4. przedstawiono wykresy różnych zależności.





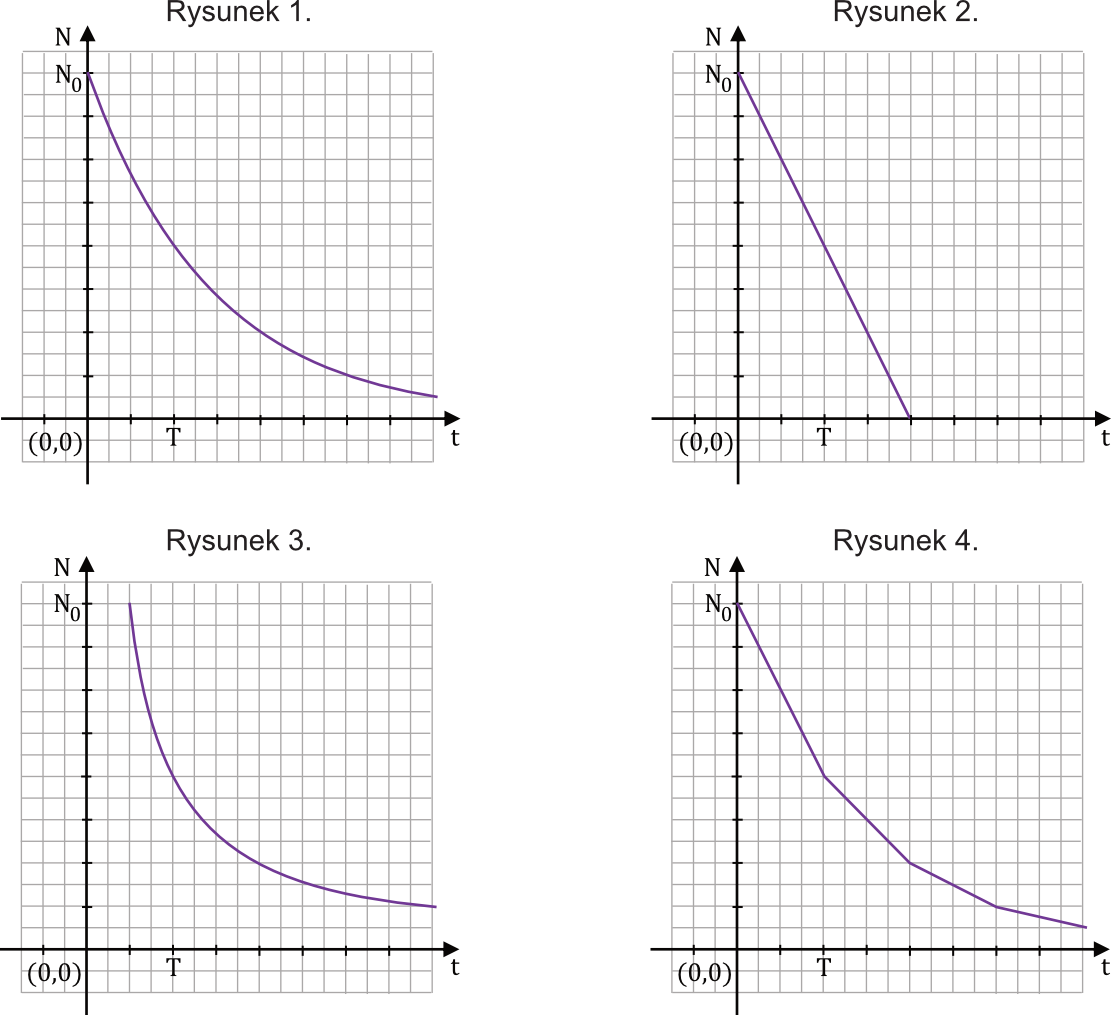
Wykres zależności wykładniczej \(N(t)\) - opisanej we wstępie do zadania - przedstawiono na

A. rysunku 1

B. rysunku 2

C. rysunku 3

D. rysunku 4



Zadanie 2.

Czas połowicznego rozpadu węgla \(^{14}C\) to około \(5700\) lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla \(^{14}C\) w pewnym organicznym znalezisku archeologicznym \(\frac{1}{16}\) masy tego izotopu, jaka utrzymywała się podczas życia organizmu.



Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.

Odpowiedź:      

1. A
2. \(22800\) lat

Rozwiązanie:      
Zadanie 1. Naszym zadaniem jest poprawne dopasowanie wykresu funkcji wykładniczej. I tu od razu nasz wzrok musimy kierować w stronę rysunku 1 oraz 3 - bowiem tak właśnie wyglądają wykresy funkcji wykładniczych typu \(y=a^x\), gdy \(0\lt a\lt1\) (w naszym przypadku \(a=\frac{1}{2}\)). Ustalmy zatem teraz, który z tych wykresów jest prawidłowy. Widzimy wyraźnie, że sytuacja z trzeciego rysunku musi zostać przez nas odrzucona, ponieważ nasz wykres musi zaczynać się od punktu \((0;0)\) i to właśnie w tym momencie musimy mieć początkową liczbę jąder naszego izotopu. Na trzecim wykresie funkcja ta jest nieco przesunięta w prawo, przez co początkowa liczba jąder izotopu przypada na czas \(\frac{1}{2}T\). W związku z tym poprawnym wykresem jest jedynie ten z pierwszej odpowiedzi. Możemy to jeszcze sobie zweryfikować, widząc że dla czasu \(T\) nasza funkcja przyjmuje połowę wartości \(N_{0}\), a dla np. \(2T\) przyjmuje jedną czwartą wartości \(N_{0}\). Zadanie 2. Do zadania można podejść na różne sposoby, ale najprościej będzie zapisać to w następujący sposób: \(m\) - początkowa masa izotopu węgla \(\frac{1}{2}m\) - masa izotopu węgla po upływie \(1T\), czyli \(5700\) lat \(\frac{1}{4}m\) - masa izotopu węgla po upływie \(2T\), czyli \(11400\) lat \(\frac{1}{8}m\) - masa izotopu węgla po upływie \(3T\), czyli \(17100\) lat \(\frac{1}{16}m\) - masa izotopu węgla po upływie \(4T\), czyli \(22800\) lat To oznacza, że znalezisko archeologiczne ma \(22800\) lat.

Teoria:      
W trakcie opracowania