Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa \(8 cm\), a długość przeciwprostokątnej jest równa \(10 cm\). Najmniejsza ściana boczna tego graniastosłupa ma pole równe \(54 cm^2\).





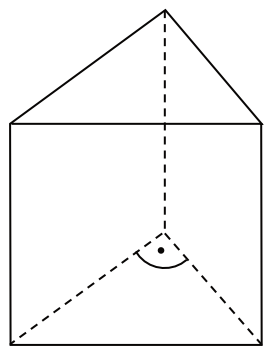
Oblicz sumę długości wszystkich krawędzi tego graniastosłupa. Zapisz obliczenia.

Odpowiedź:      

\(75cm\)

Rozwiązanie:      
Krok 1. Obliczenie długości drugiej przyprostokątnej. Z treści zadania wynika, że w podstawie graniastosłupa mamy trójkąt prostokątny, którego jedna przyprostokątna ma długość \(8cm\), a przeciwprostokątna ma długość \(10cm\). Brakującą długość drugiej przyprostokątnej możemy obliczyć z twierdzenia Pitagorasa, zatem: $$8^2+b^2=10^2 \           ,\ 64+b^2=100 \           ,\ b^2=36 \           ,\ b=6 \quad\lor\quad b=-6$$ Ujemną długość oczywiście odrzucamy, bo długość boku musi być dodatnia, stąd też \(b=6\). Warto przy okazji zauważyć, że będzie to tym samym najkrótszy bok tego trójkąta. Krok 2. Obliczenie wysokości graniastosłupa. Wiemy, że najmniejsza ściana graniastosłupa ma pole równe \(54 cm^2\). Ściana graniastosłupa jest prostokątem, w którym jeden z boków to bok trójkąta znajdującego się w podstawie, a drugi bok to wysokość graniastosłupa. Najmniejsza ściana będzie wychodzić z najkrótszego boku trójkąta, czyli boku o długości \(6cm\), zatem: $$6cm\cdot H=54cm^2 \           ,\ H=9cm$$ Krok 3. Obliczenie sumy długości krawędzi graniastosłupa. Celem zadania jest obliczenie sumy długości wszystkich krawędzi. Nasz graniastosłup ma dwie pary krawędzi o długościach \(6cm\), \(8cm\) oraz \(10cm\) (to krawędzie z trójkątów z podstawy dolnej i górnej) oraz trzy krawędzie o długości \(9cm\). W związku z tym: $$K=2\cdot(6cm+8cm+10cm)+3\cdot9cm \           ,\ K=2\cdot24cm+27cm \           ,\ K=48cm+27cm \           ,\ K=75cm$$

Teoria:      
W trakcie opracowania