Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości \(6m\) i \(16m\) oraz wysokości \(12m\). Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o \(20\%\) (szerokość wału u podnóża i na szczycie nie zmienia się).





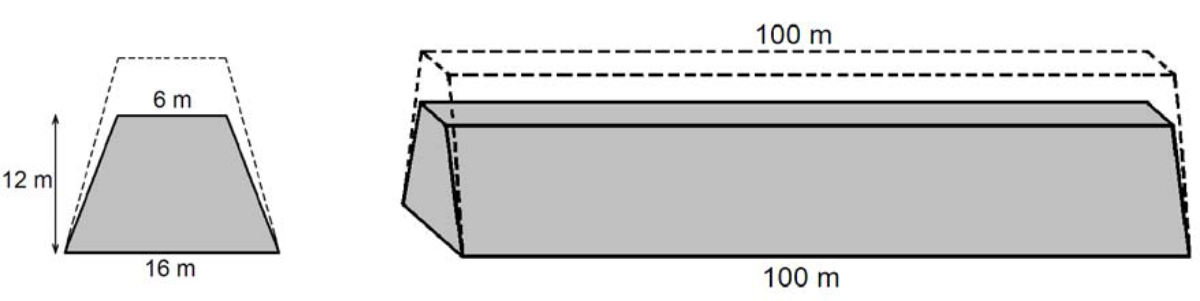
Po zakończeniu osiadania ziemi, w celu zmniejszenia przesiąkania, na zboczu wału od strony wody zostanie ułożona warstwa gliny. Oblicz pole powierzchni, którą trzeba będzie wyłożyć gliną na \(100\)-metrowym odcinku tego wału (wał ma kształt graniastosłupa prostego). Wynik podaj z jednostką.

Odpowiedź:      

\(P=1300m^2\)

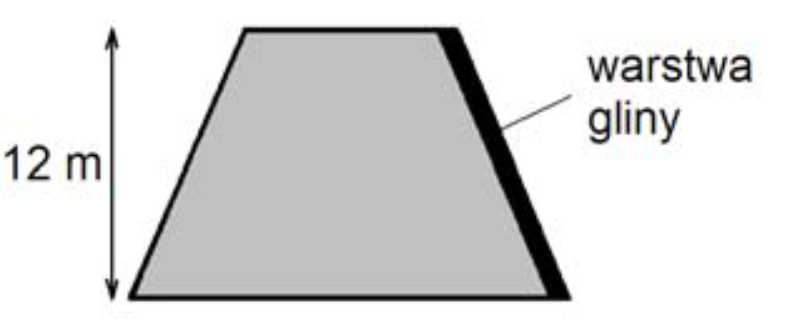
Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Z racji tego iż jest to trapez równoramienny to możemy skorzystać z jego własności i w ten sposób podzielić \(16m\) długości dolnej podstawy na odcinki o długościach \(5m, 6m, 5m\) (tak jak zaznaczono na rysunku). Krok 2. Obliczenie długości ramienia trapezu. Musimy obliczyć długość odcinka \(x\), który przyda nam się do obliczenia pola powierzchni warstwy gliny. Skorzystamy tutaj z Twierdzenia Pitagorasa i trójkąta prostokątnego o bokach \(5m\), \(12m\) oraz \(x\): $$5^2+12^2=x^2 \           ,\ 25+144=x^2 \           ,\ x^2=169 \           ,\ x=13[m]$$ Krok 3. Obliczenie pola powierzchni prostokąta. Powierzchnia zbocza wału jest prostokątem o bokach \(13m\) oraz \(100m\). To oznacza, że poszukiwane pole będzie równe: $$P=13m\cdot100m=1300m^2$$

Teoria:      
W trakcie opracowania