Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości \(6m\) i \(16m\) oraz wysokości \(12m\). Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o \(20\%\) (szerokość wału u podnóża i na szczycie nie zmienia się).





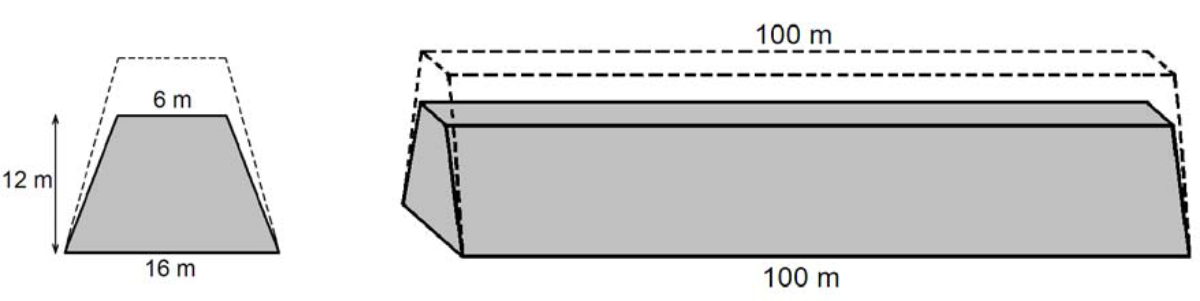
Oblicz, ile metrów sześciennych ziemi trzeba przywieźć na usypanie \(100\)-metrowego odcinka ziemnego wału przeciwpowodziowego (w kształcie graniastosłupa prostego) opisanego w informacjach.

Odpowiedź:      

Do usypania wału potrzeba \(16500m^3\) ziemi.

Rozwiązanie:      
Krok 1. Obliczenie wysokości dużego wału (świeżo usypanego). Zgodnie z rysunkiem wiemy, że docelowy wał ma \(12m\) i że stanowić on będzie \(80\%\) tego co zostanie usypane. W związku z tym możemy zapisać następujące oznaczenia: \(x\) - wysokość świeżo usypanego wału \(0,8x\) - wysokość wału docelowego Nasz wał docelowy ma \(12m\), czyli zajdzie równanie: $$0,8x=12m \           ,\ x=15m$$ To oznacza, że świeżo nasypany wał będzie mieć wysokość \(15m\). Krok 2. Obliczenie pola powierzchni przekroju dużego wału (świeżo usypanego). Ten wał jest tak naprawdę graniastosłupem o podstawie trapezowej (można go sobie obrócić by sobie to lepiej wyobrazić). Spróbujmy więc na początku obliczyć pole powierzchni tego trapezu, które będzie jednocześnie polem podstawy graniastosłupa. Przed chwilą wyliczyliśmy sobie, że jego wysokość będzie równa \(15m\), natomiast długości podstawy dolnej i górnej się nie zmienią (bo tak wynika z treści zadania). W związku z tym pole trapezu wyniesie: $$P_{p}=\frac{1}{2}(a+b)\cdot H \           ,\ P_{p}=\frac{1}{2}\cdot(16m+6m)\cdot15m \           ,\ P_{p}=\frac{1}{2}\cdot22m\cdot15m \           ,\ P_{p}=11m\cdot15m \           ,\ P_{p}=165m^2$$ Krok 3. Obliczenie objętości wału. Z racji tego iż wał ma długość \(100m\), to jego objętość będzie równa: $$V=P_{p}\cdot H \           ,\ V=165m^2\cdot100m \           ,\ V=16500m^3$$ To oznacza, że do usypania wału potrzebujemy \(16500m^3\) ziemi.

Teoria:      
W trakcie opracowania