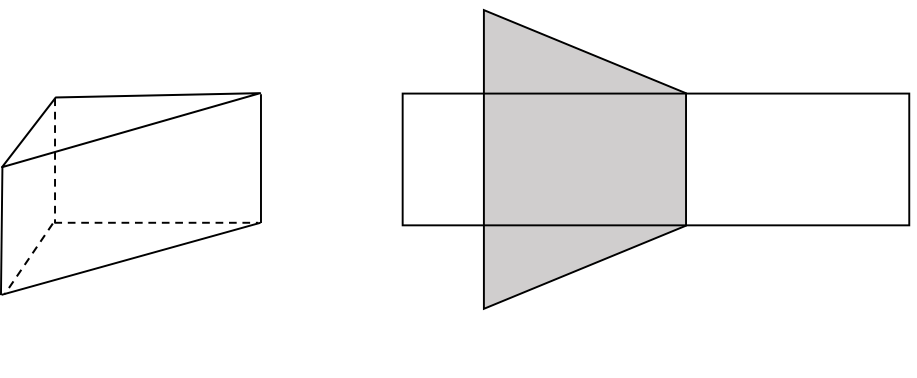
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają \(12cm\) i \(13cm\) długości, a pole zacieniowanej części siatki graniastosłupa jest równe \(168cm^2\). Oblicz objętość tego graniastosłupa.

Odpowiedź:      

Objętość graniastosłupa wynosi \(270cm^3\).

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Spróbujmy nanieść znane nam miary długości na nasz rysunek. Nanieśmy też sobie od razu informację gdzie w tej siatce znajduje się wysokość graniastosłupa, bo ona będzie nam potrzebna do obliczenia objętości. Skrzydełka na górze i na dole siatki są trójkątami prostokątnymi, który znajduje się w podstawie. Skąd jednak wiemy, że boki o długości \(12cm\) oraz \(13cm\) są podpisane dobrze, a nie np. w odwrotnej kolejności? Faktycznie nie jest to zapisane wprost który bok ma jaką długość, ale my wiemy, że długości \(12cm\) oraz \(13cm\) to najdłuższe boki trójkąta prostokątnego. W trójkącie prostokątnym najdłuższym bokiem jest zawsze przeciwprostokątna, stąd wiemy, że to ona ma konkretnie \(13cm\). Krok 2. Obliczenie długości trzeciego boku trójkąta znajdującego się w podstawie. Z treści zadania wiemy, że dwa boki trójkąta znajdującego się w podstawie mają długość \(12cm\) oraz \(13cm\). Możemy więc z Twierdzenia Pitagorasa obliczyć trzecią długość: $$x^2+12^2=13^2 \           ,\ x^2+144=169 \           ,\ x^2=25 \           ,\ x=5[cm]$$ To oznacza, że krótsza przyprostokątna (czyli najkrótsza krawędź podstawy graniastosłupa) ma długość \(5cm\). Krok 3. Obliczenie wysokości graniastosłupa. Teraz możemy przystąpić do obliczenia wysokości graniastosłupa. Jak ją wyznaczymy? Skorzystamy tutaj z tego iż zacieniowaną figurą jest trapez o polu powierzchni równym \(168cm^2\). Dolna podstawa trapezu zgodnie z rysunkiem ma długość \(5+h+5=10+h\), natomiast górna podstawa ma długość \(h\). Wysokość trapezu jest równa \(12cm\). To oznacza, że \(h\) jest już jedyną niewiadomą, zatem wyznaczymy ją w prosty sposób: $$168=\frac{1}{2}(10+h+h)\cdot12 \           ,\ 168=(2h+10)\cdot6 \           ,\ 168=12h+60 \           ,\ 108=12h \           ,\ h=9[cm]$$ Krok 4. Obliczenie pola podstawy. W podstawie mamy trójkąt prostokątny o podstawie \(12cm\) i wysokości \(5cm\). Pole podstawy będzie więc równe: $$P_{p}=\frac{1}{2}\cdot12\cdot5 \           ,\ P_{p}=6\cdot5 \           ,\ P_{p}=30[cm^2]$$ Krok 5. Obliczenie objętości graniastosłupa. Znamy już wszystkie dane. Pole podstawy jest równe \(30cm^2\), wysokość bryły wynosi \(9cm\), zatem objętość wynosi: $$V=P_{p}\cdot H \           ,\ V=30cm^2\cdot9cm \           ,\ V=270cm^3$$

Teoria:      
W trakcie opracowania