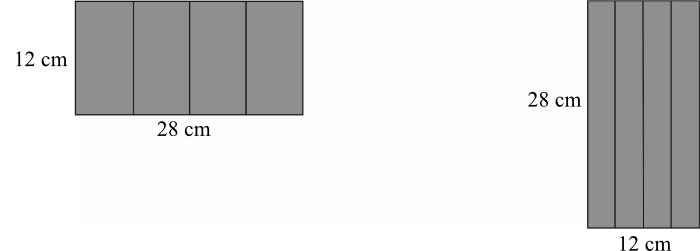
Maja zrobiła dwa pudełka w kształcie graniastosłupów prawidłowych czworokątnych o różnych objętościach. Powierzchnię boczną każdego z tych graniastosłupów wykonała z takich samych prostokątów o wymiarach \(28cm\) i \(12cm\) (patrz rysunek). Oblicz różnicę objętości tych graniastosłupów. Zapisz obliczenia.

Odpowiedź:      

\(336cm^3\)

Rozwiązanie:      
Krok 1. Obliczenie długości krawędzi podstawy i pola podstawy pierwszego graniastosłupa. Na początku obliczmy z rysunku długość krawędzi podstawy pierwszego graniastosłupa. Będzie ono równe: $$a=28cm:4=7cm$$ Znając długość krawędzi podstawy możemy obliczyć pole powierzchni graniastosłupa. Wiemy, że w podstawie graniastosłupa jest kwadrat (wynika to z faktu, że graniastosłup jest prawidłowy czworokątny). To oznacza, że pole podstawy będzie równe: $$P_{p}=a^2 \           ,\ P_{p}=7^2 \           ,\ P_{p}=49[cm^2]$$ Krok 2. Obliczenie objętości pierwszego graniastosłupa. Objętość graniastosłupa wyliczymy ze wzoru: $$V=P_{p}\cdot H$$ Pole podstawy jest już nam znane (\(P_{p}=49cm^2\)), wysokość bryły możemy odczytać z rysunku (\(H=12cm\)), zatem objętość graniastosłupa będzie równa: $$V_{1}=49\cdot12 \           ,\ V_{1}=588[cm^3]$$ Krok 3. Obliczenie długości krawędzi bocznej i pola podstawy drugiego graniastosłupa. Długość krawędzi podstawy drugiego graniastosłupa jest równa: $$a=12cm:4=3cm$$ To oznacza, że pole podstawy będzie równe: $$P_{p}=a^2 \           ,\ P_{p}=3^2 \           ,\ P_{p}=9[cm^2]$$ Krok 4. Obliczenie objętości drugiego graniastosłupa. Skoro \(P_{p}=9cm\) oraz \(H=28cm\), to objętość drugiego ostrosłupa będzie równa: $$V_{2}=P_{p}\cdot H \           ,\ V_{2}=9\cdot28 \           ,\ V_{2}=252[cm^3]$$ Krok 5. Obliczenie różnicy objętości między pierwszym i drugim graniastosłupem. Znając objętość jednego i drugiego graniastosłupa możemy obliczyć różnicę tych objętości: $$V_{1}-V_{2}=588cm^3-252cm^3=336cm^3$$

Teoria:      
W trakcie opracowania