Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.





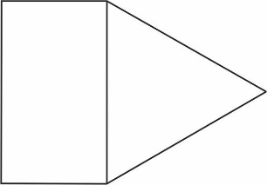
Pole narysowanego trójkąta jest równe \(16\sqrt{3}cm^2\), a pole prostokąta jest równe \(24\sqrt{3}cm^2\). Oblicz objętość tego graniastosłupa.

Odpowiedź:      

\(144cm^3\)

Rozwiązanie:      
Krok 1. Obliczenie długości krawędzi podstawy graniastosłupa. Z treści zadania wiemy, że jest to graniastosłup prawidłowy trójkątny, czyli w podstawie tej bryły znajduje się trójkąt równoboczny. To bardzo ważna informacja, bowiem dzięki niej wiemy, że trójkąt z naszej siatki jest na pewno równoboczny, a to oznacza że możemy obliczyć długość jego boku. W tym celu skorzystamy ze wzoru \(P=\frac{a^2\cdot\sqrt{3}}{4}\). Mamy podane, że pole tego trójkąta jest równe \(P=16\sqrt{3}cm^2\), zatem podstawiając tę informację do naszego wzoru otrzymamy równanie: $$\frac{a^2\cdot\sqrt{3}}{4}=16\sqrt{3}cm^2 \quad\bigg/\cdot4 \           ,\ a^2\cdot\sqrt{3}=64\sqrt{3}cm^2 \quad\bigg/:\sqrt{3} \           ,\ a^2=64cm^2 \           ,\ a=8cm$$ To oznacza, że trójkąt z naszej siatki ma wszystkie boki równe \(8cm\). Krok 2. Obliczenie wysokości graniastosłupa. W ścianie bocznej mamy prostokąt. Jedna z długości tego prostokąta pokrywa się z długością krawędzi trójkąta, czyli wiemy że ma ona długość \(a=8cm\). Musimy obliczyć teraz długość drugiego boku tego prostokąta, który będzie tak naprawdę wysokością całego graniastosłupa. Tę długość obliczymy korzystając z informacji o polu powierzchni. W ścianie bocznej jest prostokąt o polu \(24\sqrt{3}cm^2\), zatem: $$a\cdot b=24\sqrt{3}cm^2 \           ,\ 8cm\cdot b=24\sqrt{3}cm^2 \           ,\ b=3\sqrt{3}cm$$ Krok 3. Obliczenie objętości graniastosłupa. Do obliczenia objętości graniastosłupa potrzebujemy znać pole podstawy oraz wysokość bryły. Pole podstawy już znamy, bo jest to po prostu pole naszego trójkąta, czyli \(16\sqrt{3}cm^2\), a wysokość to obliczone przed chwilą \(3\sqrt{3}cm\). Zatem: $$V=P_{p}\cdot H \           ,\ V=16\sqrt{3}cm^2 \cdot 3\sqrt{3}cm \           ,\ V=48\cdot3cm^3 \           ,\ V=144cm^3$$

Teoria:      
W trakcie opracowania