Na rysunku I przedstawiono graniastosłup prawidłowy, którego wszystkie krawędzie są przystające, a suma ich długości wynosi \(90cm\). Na II rysunku przedstawiono graniastosłup, który ma w podstawie trójkąt prostokątny o przyprostokątnych długości \(6cm\) i \(8cm\). Obie bryły mają taką samą wysokość.





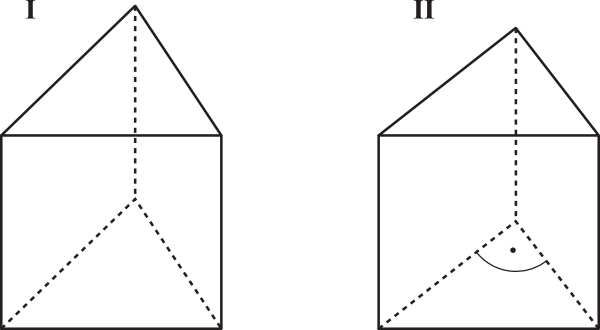
Oba te graniastosłupy połączono w taki sposób, że otrzymano jeden graniastosłup czworokątny. Oblicz pole powierzchni całkowitej otrzymanego graniastosłupa czworokątnego. Zapisz obliczenia.

Odpowiedź:      

\(P=388+50\sqrt{3}cm^2\)

Rozwiązanie:      
Krok 1. Obliczenie długości krawędzi pierwszego graniastosłupa. Z treści zadania wynika, że krawędzie pierwszego graniastosłupa są przystające, czyli mają jednakową miarę. Nasz graniastosłup ma \(9\) krawędzi, a skoro suma ich długości jest równa \(90cm\), to każda krawędź na długość: $$a=90cm:9 \           ,\ a=10cm$$ Krok 2. Obliczenie długości nieznanej krawędzi podstawy drugiego graniastosłupa. O drugim graniastosłupie wiemy to, że w podstawie jest trójkąt prostokątny o przyprostokątnych długości \(6cm\) oraz \(8cm\). Korzystając więc z Twierdzenia Pitagorasa możemy obliczyć długość przeciwprostokątnej (czyli trzeciej krawędzi podstawy), zatem: $$a^2+b^2=c^2 \           ,\ 6^2+8^2=c^2 \           ,\ 36+64=c^2 \           ,\ c^2=100 \           ,\ c=10[cm]$$ Krok 3. Ustalenie wyglądu bryły po połączeniu graniastosłupów. Ustalmy jak będzie wyglądać nasza bryła, która powstanie po połączeniu się pierwszego i drugiego graniastosłupa. Skoro mamy otrzymać graniastosłup czworokątny, to te dwa graniastosłupy trzeba będzie połączyć wzdłuż boku o jednakowej mierze, czyli w tym przypadku wzdłuż boku o długości \(10cm\). Każde inne złączenie spowoduje, że w podstawie nie będziemy mieli czworokąta. Wiemy też, że nowo powstała bryła ma wysokość \(10cm\), bo tak wynika z informacji na temat pierwszego graniastosłupa. W związku z tym nasz graniastosłup będzie wyglądać mniej więcej w ten sposób: Krok 4. Obliczenie pól podstawy pierwszego i drugiego graniastosłupa. Pole podstawy nowego graniastosłupa jest sumą pól podstaw pierwszego i drugiego graniastosłupa. Musimy zatem wyliczyć te dwa pola i je ze sobą zsumować. W pierwszej podstawie mamy trójkąt równoboczny o boku \(a=10cm\). Pole pierwszego graniastosłupa jest więc proste do policzenia jeśli znamy wzór na pole trójkąta równobocznego \(P=\frac{a^2\sqrt{3}}{4}\). Wystarczy wtedy podstawić znaną nam miarę o otrzymamy, że: $$P_{p1}=\frac{10^2\cdot\sqrt{3}}{4} \           ,\ P_{p1}=\frac{100\sqrt{3}}{4} \           ,\ P_{p1}=25\sqrt{3}[cm^2]$$ Niestety w niektórych szkołach ten wzór nie jest omawiamy, ale omawiany jest za to wzór na wysokość trójkąta równobocznego \(h=\frac{a\sqrt{3}}{2}\) i dzięki niemu także możemy obliczyć pole powierzchni. Obliczmy zatem wysokość naszego trójkąta równobocznego o boku \(a=10cm\): $$h=\frac{10\cdot\sqrt{3}}{2} \           ,\ h=5\sqrt{3}[cm]$$ Teraz korzystając ze standardowego wzoru na pole trójkąta możemy zapisać, że: $$P_{p1}=\frac{1}{2}ah \           ,\ P_{p1}=\frac{1}{2}\cdot10\cdot5\sqrt{3} \           ,\ P_{p1}=5\cdot5\sqrt{3} \           ,\ P_{p1}=25\sqrt{3}[cm^2]$$ Obliczenie pola powierzchni podstawy drugiego graniastosłupa jest już mniej problematyczne, bo z własności trójkątów prostokątnych wiemy, że przyprostokątne takiego trójkąta są jednocześnie długościami podstawy i wysokości trójkąta, zatem: $$P_{p2}=\frac{1}{2}ah \           ,\ P_{p2}=\frac{1}{2}\cdot6\cdot8 \           ,\ P_{p2}=3\cdot8 \           ,\ P_{p2}=24[cm^2]$$ Krok 5. Obliczenie pola powierzchni bocznej graniastosłupa czworokątnego. Mamy cztery ściany boczne, każda z nich jest prostokątem o wysokości \(10cm\). Zgodnie z naszym rysunkiem możemy zapisać, że: $$P_{b}=6\cdot10+8\cdot10+10\cdot10+10\cdot10 \           ,\ P_{b}=60+80+100+100 \           ,\ P_{b}=340[cm^2]$$ Krok 6. Obliczenie pola powierzchni całkowitej graniastosłupa czworokątnego. Pole podstawy nowo powstałego graniastosłupa to suma obliczonych w czwartym kroku pól \(P_{p1}\) oraz \(P_{p2}\). Pole powierzchni bocznej obliczyliśmy w kroku piątym. Jesteśmy więc gotowi do obliczenia pola powierzchni całkowitej, ale musimy pamiętać o tym, by pole podstawy graniastosłupa czworokątnego pomnożyć przez \(2\), bo graniastosłup ma przecież podstawę dolną i górną. Zatem: $$P=2\cdot(P_{p1}+P_{p2})+P_{b} \           ,\ P=2\cdot(25\sqrt{3}+24)+340 \           ,\ P=50\sqrt{3}+48+340 \           ,\ P=388+50\sqrt{3}[cm^2]$$

Teoria:      
W trakcie opracowania