Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Egzamin ósmoklasisty 2022 - matematyka Zadanie 19 z 8434
Zadanie nr 19. (3pkt)
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
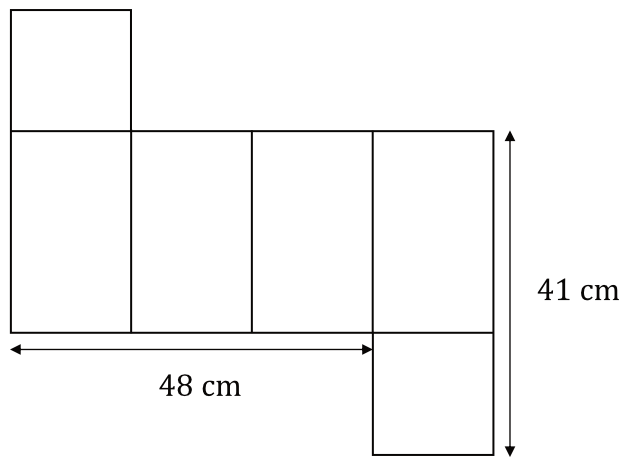
Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
Odpowiedź:
\(V=6400cm^3\)
Rozwiązanie:
Krok 1. Obliczenie wymiarów graniastosłupa.
Spójrzmy na odcinek o długości \(48cm\). Składa się on z trzech jednakowych prostokątów, które są ścianami bocznymi naszej bryły (na pewno są one jednakowe, bo graniastosłup jest prawidłowy, czyli wszystkie ściany boczne są takie same). To oznacza, że krótsza długość pojedynczego prostokąta wynosi:
$$48cm:3=16cm$$
To prowadzi nas do wniosku, że w podstawie znajdzie się kwadrat o boku \(16cm\) (musi to być kwadrat, bo graniastosłup jest prawidłowy). Skoro tak, to wysokość bryły będzie równa:
$$41cm-16cm=25cm$$
Dobrze będzie to wszystko widać na rysunku pomocniczym:
Krok 2. Obliczenie pola podstawy.
W podstawie bryły mamy kwadrat o boku \(16cm\), zatem pole podstawy będzie równe:
$$P_{p}=16cm\cdot16cm \ ,\
P_{p}=256cm$$
Krok 3. Obliczenie objętści.
Wiemy już, że \(P_{p}=256cm\) i wyznaczyliśmy sobie, że \(H=25cm\). W związku z tym objętość graniastosłupa będzie równa:
$$V=P_{p}\cdot H \ ,\
V=256cm^2\cdot25 \ ,\
V=6400cm^3$$
Teoria:
W trakcie opracowania
CKE

