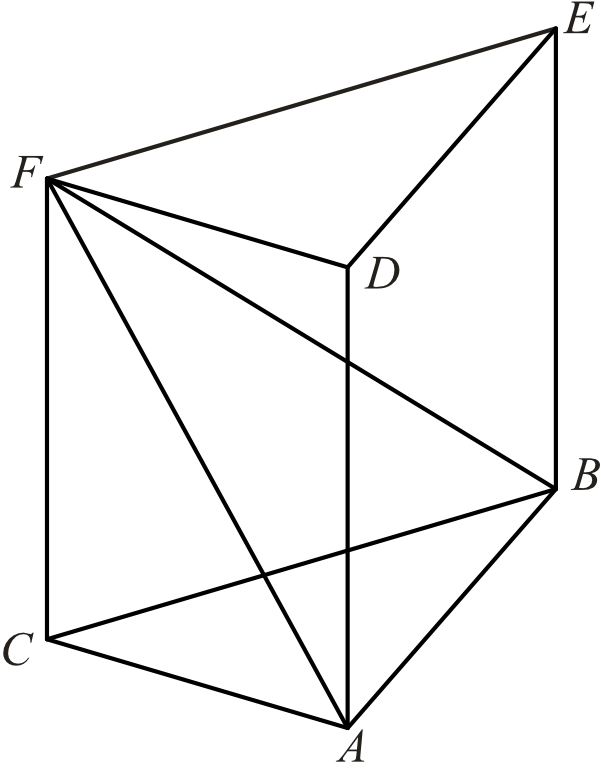
Dany jest graniastosłup prawidłowy trójkątny \(ABCDEF\) o podstawach \(ABC\) i \(DEF\) i krawędziach bocznych \(AD\), \(BE\) i \(CF\) (zobacz rysunek). Długość krawędzi podstawy \(AB\) jest równa \(8\), a pole trójkąta \(ABF\) jest równe \(52\). Oblicz objętość tego graniastosłupa.

Odpowiedź:      

\(V=176\sqrt{3}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Dorysujmy do głównego rysunku dwie wysokości - pierwszą niech będzie wysokość trójkąta \(ABC\) oraz drugą, tym razem trójkąta \(ABF\). Dodatkowo podpiszmy długości poszczególnych boków, a skoro jest to graniastosłup prawidłowy trójkątny, to w podstawie mamy trójkąt równoboczny, czyli więc wszystkie krawędzie podstawy mają długość \(8\). Krok 2. Obliczenie długości wysokości trójkąta \(ABF\), czyli odcinka \(FG\). Możemy dostrzec, że trójkąt \(ABF\) jest trójkątem równoramiennym (obydwa ramiona są przekątnymi identycznych ścian bocznych). Korzystając więc z pola trójkąta podanego w treści zadania (\(P=52\)) oraz długości podstawy trójkąta (\(a=8\)) możemy obliczyć wysokość trójkąta \(ABF\): $$P=\frac{1}{2}a\cdot h_{1} \           ,\ 52=\frac{1}{2}\cdot8\cdot h_{1} \           ,\ 52=4h_{1} \           ,\ h_{1}=13$$ Wysokość \(|FG|\) jest więc równa \(13\). Krok 3. Obliczenie długości wysokości trójkąta \(ABC\), czyli odcinka \(CG\). Jak już sobie ustaliliśmy - w podstawie jest trójkąt równoboczny o boku długości \(a=8\). Jego wysokość możemy więc obliczyć korzystając z następującego wzoru: $$h_{2}=\frac{a\sqrt{3}}{2} \           ,\ h_{2}=\frac{8\sqrt{3}}{2} \           ,\ h_{2}=4\sqrt{3}$$ Wysokość \(|CG|\) jest więc równa \(4\sqrt{3}\). Krok 4. Obliczenie wysokości graniastosłupa, czyli odcinka \(FC\). Do obliczenia objętości potrzebna nam jest oczywiście wysokość graniastosłupa. Wyznaczymy ją przy pomocy Twierdzenia Pitagorasa z trójkąta \(FCG\): $$|FC|^2+|CG|^2=|FG|^2 \           ,\ |FC|^2+(4\sqrt{3})^2=13^2 \           ,\ |FC|^2+16\cdot3=169 \           ,\ |FC|^2+48=169 \           ,\ |FC|^2=121 \           ,\ |FC|=11$$ Wysokość całego graniastosłupa jest więc równa \(H=11\). Krok 5. Obliczenie pola podstawy. Skoro w podstawie znajduje się trójkąt równoboczny, to jego pole jest równe: $$P=\frac{a^2\sqrt{3}}{4} \           ,\ P=\frac{8^2\sqrt{3}}{4} \           ,\ P=\frac{64\sqrt{3}}{4} \           ,\ P=16\sqrt{3}$$ Krok 6. Obliczenie objętości graniastosłupa. Mamy już wszystkie dane, tak więc możemy przystąpić do obliczenia objętości: $$V=P_{p}\cdot H \           ,\ V=16\sqrt{3}\cdot11 \           ,\ V=176\sqrt{3}$$

Teoria:      
W trakcie opracowania