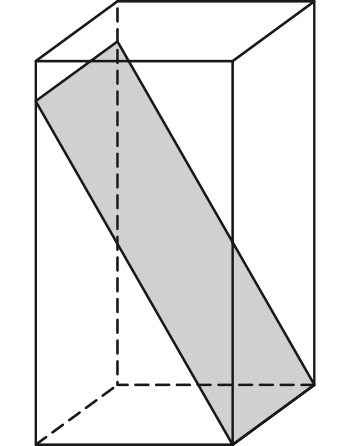
Krawędź podstawy graniastosłupa prawidłowego czworokątnego jest równa \(1\). Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i tworzącą z tą podstawą kąt \(60°\) (zobacz rysunek). Oblicz pole otrzymanego przekroju.

A \(1\)
B \(\frac{2\sqrt{3}}{3}\)
C \(\sqrt{3}\)
D \(2\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Nanieśmy na rysunek dane z treści zadania i przy okazji zaznaczmy kluczowy trójkąt prostokątny: Krok 2. Obliczenie długości drugiego boku prostokąta. Drugi bok prostokątna jest przeciwprostokątną naszego zaznaczonego powyżej trójkąta prostokątnego. Korzystając z funkcji trygonometrycznych możemy zapisać, że: $$cos60°=\frac{1}{x} \           ,\ \frac{1}{2}=\frac{1}{x} \           ,\ x=2$$ Krok 3. Obliczenie pola powierzchni otrzymanego przekroju. Nasz przekrój jest prostokątem o wymiarach \(1\times2\), zatem: $$P=1\cdot2 \           ,\ P=2$$

Teoria:      
W trakcie opracowania