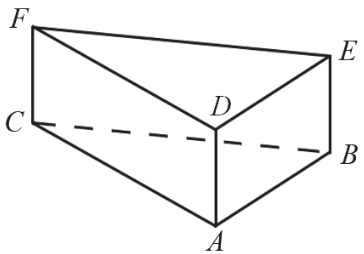
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Pole powierzchni całkowitej tego graniastosłupa jest równe \(45\sqrt{3}\). Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz objętość tego graniastosłupa.

Odpowiedź:      

\(V=\frac{81}{2}\)

Rozwiązanie:      
Krok 1. Obliczenie pola podstawy graniastosłupa. Z treści zadania wynika, że pole podstawy (czyli \(P_{p}\)) jest dokładnie takie samo jak pole ściany bocznej (które oznaczymy sobie jako \(P_{śb}\)). Skoro więc \(P_{p}=P_{śb}\) to korzystając ze wzoru na pole powierzchni całkowitej możemy zapisać, że: $$P_{c}=2P_{p}+3P_{śb} \           ,\ P_{c}=2P_{p}+3P_{p} \           ,\ P_{c}=5P_{p} \           ,\ 45\sqrt{3}=5P_{p} \           ,\ P_{p}=9\sqrt{3}$$ Krok 2. Obliczenie długości krawędzi podstawy. Skoro w podstawie jest trójkąt równoboczny i skoro znamy jego pole powierzchni (obliczyliśmy je przed chwilą) to w prosty sposób możemy obliczyć także długość krawędzi podstawy: $$P=\frac{a^2\sqrt{3}}{4} \           ,\ 9\sqrt{3}=\frac{a^2\sqrt{3}}{4} \quad\bigg/\cdot4 \           ,\ 36\sqrt{3}=a^2\sqrt{3} \quad\bigg/:\sqrt{3} \           ,\ a^2=36 \           ,\ a=6 \quad\lor\quad a=-6$$ Wartość ujemną oczywiście odrzucamy, bo długość boku nie może być ujemna. Zostaje nam zatem \(a=6\). Krok 3. Obliczenie wysokości graniastosłupa. Wysokość graniastosłupa jest jednocześnie wysokością ściany bocznej. O tej ścianie bocznej wiemy, że jest prostokątem o polu powierzchni \(9\sqrt{3}\) (bo jest to takie samo pole co pole podstawy). Skoro więc znamy miarę jednego boku tego prostokąta \(a=6\), to drugi bok (będący jednocześnie wysokością graniastosłupa) jest już bardzo prosty do policzenia: $$P_{śb}=a\cdot H \           ,\ 9\sqrt{3}=6\cdot H \           ,\ H=\frac{3}{2}\sqrt{3}$$ Krok 4. Obliczenie objętości graniastosłupa. Mamy już wszystkie potrzebne dane do obliczenia objętości, zatem: $$V=P_{p}\cdot H \           ,\ V=9\sqrt{3}\cdot\frac{3}{2}\sqrt{3} \           ,\ V=\frac{27}{2}\cdot3 \           ,\ V=\frac{81}{2}$$

Teoria:      
W trakcie opracowania