Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura z matematyki (poziom podstawowy) - Maj 2018 Zadanie 21 z 1044
Zadanie nr 21. (1pkt)
Podstawą graniastosłupa prostego jest prostokąt o bokach długości \(3\) i \(4\). Kąt \(α\), jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy \(45°\) (zobacz rysunek).
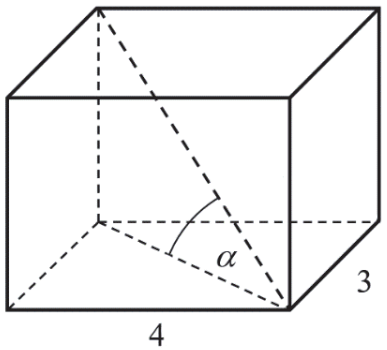
Wysokość graniastosłupa jest równa:
A \(5\)
B \(3\sqrt{2}\)
C \(5\sqrt{2}\)
D \(\frac{5\sqrt{3}}{3}\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Skąd wiemy, że kąt \(DHB\) ma miarę \(45°\)? Skoro kąt \(α\) ma miarę \(45°\), a trójkąt \(DBH\) jest trójkątem prostokątnym, to znaczy że drugi kąt ostry w zaznaczonym trójkącie musi mieć także \(45°\). To z kolei oznacza, że trójkąt \(DBH\) jest równoramienny.
Krok 2. Oblicznie wysokości graniastosłupa.
Trójkąt \(DBH\) jest trójkątem równoramiennym, zatem \(|DB|=|DH|\). Długość odcinka \(DB\) (czyli przekątnej podstawy) obliczymy z Twierdzenia Pitagorasa:
$$3^2+4^2=|DB|^2 \ ,\
9+16=|DB|^2 \ ,\
|DB|^2=25 \ ,\
|DB|=5 \quad\lor\quad |DB|=-5$$
Wartość ujemną odrzucamy, bo długość boku nie może być ujemna. To oznacza, że \(|DB|=5\), czyli wysokość graniastosłupa ma także długość równą \(h=5\).
Teoria:
W trakcie opracowania
matura - CKE

