Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura z matematyki (poziom podstawowy) - Czerwiec 2020 Zadanie 19 z 658
Zadanie nr 19. (1pkt)
Dany jest trójkąt prostokątny o kątach ostrych \(α\) i \(\beta\) (zobacz rysunek).
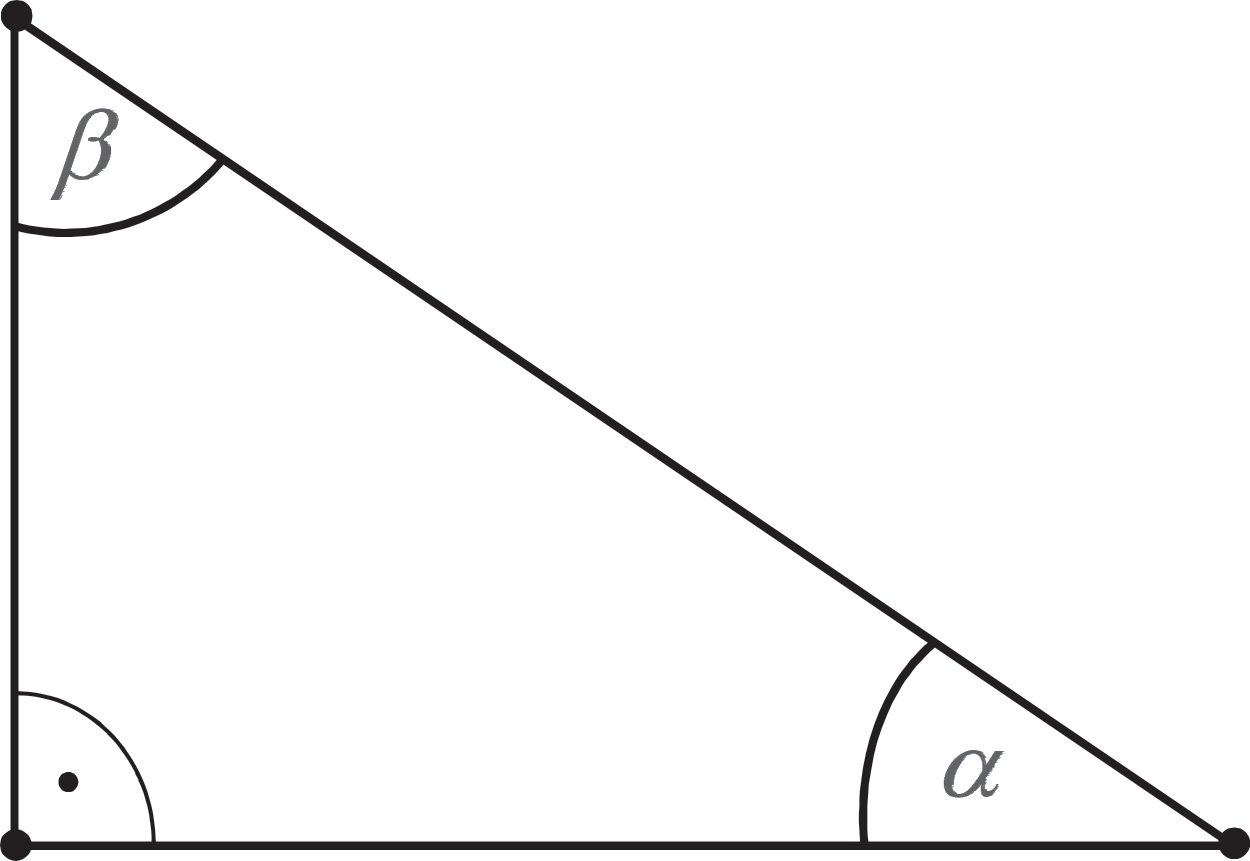
Wyrażenie \(2cosα-sin\beta\) jest równe:
A \(2sin\beta\)
B \(cosα\)
C \(0\)
D \(2\)
Rozwiązanie:
Krok 1. Wprowadzenie oznaczeń do treści zadania.
Podpiszmy poszczególne boki trójkąta jako \(a\), \(b\) oraz \(c\):
Krok 2. Rozpisanie wartości wyrażenia.
Zgodnie z oznaczeniami na naszym rysunku \(cosα=\frac{a}{c}\) natomiast \(sin\beta=\frac{a}{c}\). Otrzymujemy więc następujące równanie:
$$2cosα-sin\beta=2\cdot\frac{a}{c}-\frac{a}{c}=\frac{a}{c}$$
Zapisaliśmy sobie wcześniej, że \(\frac{a}{c}\) jest równe \(cosα\), zatem całe wyrażenie jest równe właśnie \(cosα\).
Teoria:
W trakcie opracowania
matura - CKE

