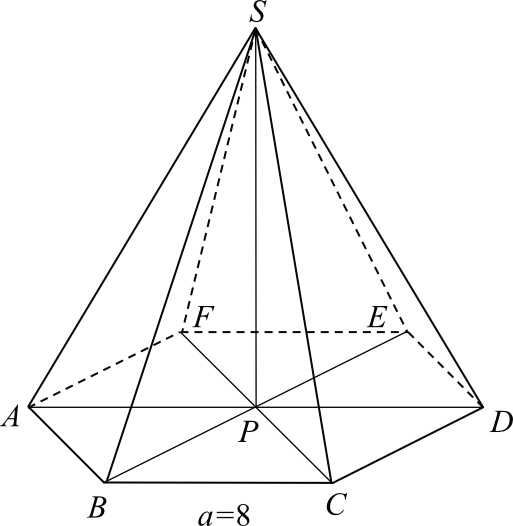
W ostrosłupie prawidłowym sześciokątnym \(ABCDEFS\), którego krawędź podstawy \(a\) ma długość \(8\) (zobacz rysunek), ściana boczna jest nachylona do płaszczyzny podstawy pod kątem \(\alpha=60°\). Oblicz cosinus kąta między krawędzią boczną a płaszczyzną podstawy tego ostrosłupa.

Odpowiedź:      

\(cos\alpha=\frac{2\sqrt{13}}{13}\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zaznaczmy znany nam kąt o mierze \(60°\) oraz kąt, którego cosinus musimy policzyć: Z własności sześciokątów wiemy, że przekątne dzielą nam taki sześciokąt na sześć jednakowych trójkątów równobocznych, a każdy z nich ma bok o długości \(a=8\). Krok 2. Obliczenie długości odcinka \(x\). Na naszym rysunku odcinek \(x\) jest wysokością trójkąta równobocznego, której potrzebujemy do dalszych obliczeń. Korzystając ze wzoru na wysokość trójkątów równobocznych możemy zapisać, że: $$h=\frac{a\sqrt{3}}{2} \           ,\ h=\frac{8\sqrt{3}}{2} \           ,\ h=4\sqrt{3}$$ Krok 3. Obliczenie wysokości ostrosłupa. Spójrzmy na niebieski trójkąt prostokątny. Znamy długość dolnej przyprostokątnej oraz kąt przy niej leżący. Korzystając z tangensa możemy zatem zapisać, że: $$tg60°=\frac{H}{4\sqrt{3}} \           ,\ \sqrt{3}=\frac{H}{4\sqrt{3}} \           ,\ H=\sqrt{3}\cdot4\sqrt{3} \           ,\ H=4\cdot3 \           ,\ H=12$$ Krok 4. Obliczenie długości krawędzi bocznej ostrosłupa. Tym razem spoglądamy na zielony trójkąt prostokątny. Znamy długości dwóch przyprostokątnych tego trójkąta, zatem korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$8^2+12^2=c^2 \           ,\ 64+144=c^2 \           ,\ c^2=208 \           ,\ c=\sqrt{208} \quad\lor\quad c=-\sqrt{208}$$ Ujemną długość oczywiście odrzucamy, bo długość boku nie może być ujemna. Zostaje nam zatem \(c=\sqrt{208}\), co możemy jeszcze rozpisać jako \(c=\sqrt{16\cdot13}=4\sqrt{13}\). Krok 5. Obliczenie cosinusa kąta między krawędzią boczną a płaszczyzną podstawy. Ponownie spoglądamy na nasz zielony trójkąt, bowiem to tu musimy wyznaczyć poszukiwany cosinus kąta między krawędzią boczną a płaszczyzną podstawy. Możemy więc zapisać, że: $$cos\alpha=\frac{8}{4\sqrt{13}} \           ,\ cos\alpha=\frac{2}{\sqrt{13}} \           ,\ cos\alpha=\frac{2\cdot\sqrt{13}}{\sqrt{13}\cdot\sqrt{13}} \           ,\ cos\alpha=\frac{2\sqrt{13}}{13}$$

Teoria:      
W trakcie opracowania