W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego \(α\) jest równy:

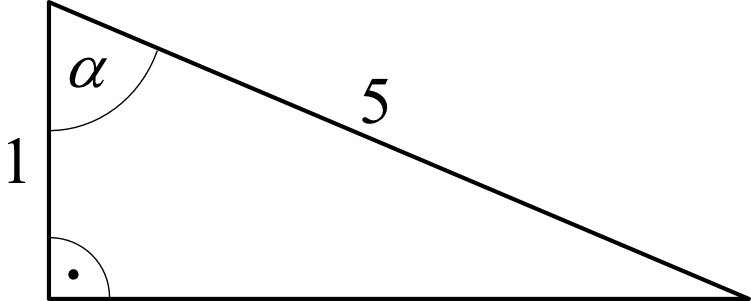
A \(\frac{1}{5}\)
B \(\frac{\sqrt{6}}{12}\)
C \(\frac{5}{24}\)
D \(\frac{2\sqrt{6}}{5}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Wyznaczenie długości drugiej przyprostokątnej. Do wyznaczenia wartości sinusa kąta ostrego \(α\) potrzebujemy znać długość przyprostokątnej leżącej naprzeciw tego kąta. Tą długość wyznaczymy z Twierdzenia Pitagorasa: $$a^2+b^2=c^2 \           ,\ 1^2+b^2=5^2 \           ,\ 1+b^2=25 \           ,\ b^2=24 \           ,\ b=\sqrt{24}=\sqrt{4\cdot6}=2\sqrt{6}$$ Krok 2. Obliczenie wartości sinusa kąta \(α\). $$sinα=\frac{2\sqrt{6}}{5}$$

Teoria:      
W trakcie opracowania