Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Nowa Era 2016 Zadanie 15 z 1428
Zadanie nr 15. (1pkt)
Kąt \(α\) jest kątem ostrym w trójkącie prostokątnym przedstawionym na rysunku.
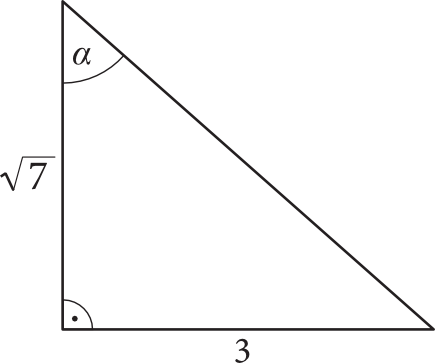
Liczba \(4^{sinα}\) jest równa:
A \(\sqrt{2^{\sqrt{7}}}\)
B \(2\sqrt{2}\)
C \(4^{\frac{3}{\sqrt{7}}}\)
D \(4\sqrt[3]{4}\)
Rozwiązanie:
Krok 1. Obliczenie długości przeciwprostokątnej.
Do obliczenia sinusa będziemy potrzebowali znać długość przeciwprostokątnej, zatem korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$3^2+(\sqrt{7})^2=c^2 \ ,\
9+7=c^2 \ ,\
c^2=16 \ ,\
c=4 \quad\lor\quad c=-4$$
Długość przeciwprostokątnej nie może być ujemna, zatem zostaje nam \(c=4\).
Krok 2. Obliczenie wartości sinusa.
Sinus opisuje nam stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) do długości przeciwprostokątnej, czyli:
$$sinα=\frac{3}{4}$$
Krok 3. Obliczenie wartości wskazanej liczby.
Naszym zadaniem jest teraz obliczenie wartości liczby \(4^{sinα}\), czyli \(4^{\frac{3}{4}}\). Korzystając z własności potęg i pierwiastków możemy zapisać, że:
$$4^{\frac{3}{4}}=\sqrt[4]{4^3}=\sqrt[4]{64}=\sqrt[4]{16\cdot4}=2\sqrt[4]{4}=2\sqrt[4]{2^2}=2\sqrt{2}$$
Teoria:
W trakcie opracowania
matura próbna - Nowa Era

